
题目列表(包括答案和解析)
如图,D,E分别是△ABC边AB,AC的中点,直线DE交△ABC的外接圆与F,G两点,若CF∥AB,证明:

(Ⅰ) CD=BC;
(Ⅱ)△BCD∽△GBD.
【命题意图】本题主要考查线线平行判定、三角形相似的判定等基础知识,是简单题.
【解析】(Ⅰ) ∵D,E分别为AB,AC的中点,∴DE∥BC,
∵CF∥AB, ∴BCFD是平行四边形,
∴CF=BD=AD, 连结AF,∴ADCF是平行四边形,

∴CD=AF,
∵CF∥AB, ∴BC=AF, ∴CD=BC;
(Ⅱ) ∵FG∥BC,∴GB=CF,
由(Ⅰ)可知BD=CF,∴GB=BD,
∵∠DGB=∠EFC=∠DBC, ∴△BCD∽△GBD
已知函数 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时, =
= ,
,
当 ≤2时,由
≤2时,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
当2< <3时,
<3时, ≥3,无解;
≥3,无解;
当 ≥3时,由
≥3时,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集为{
≥3的解集为{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
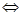
 ,
,
当 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
已知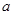 ,
,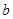 ,
,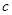 分别为
分别为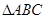 三个内角
三个内角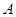 ,
,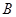 ,
,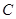 的对边,
的对边, .
.
(Ⅰ)求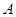 ;
;
(Ⅱ)若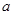 =2,
=2,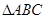 的面积为
的面积为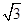 ,求
,求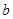 ,
,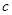 .
.
【命题意图】本题主要考查正余弦定理应用,是简单题.
【解析】(Ⅰ)由 及正弦定理得
及正弦定理得
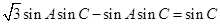
由于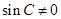 ,所以
,所以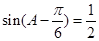 ,
,
又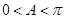 ,故
,故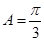 .
.
(Ⅱ) 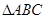 的面积
的面积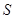 =
=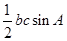 =
=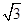 ,故
,故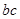 =4,
=4,
而 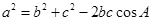 故
故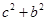 =8,解得
=8,解得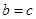 =2
=2
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。如果当天卖不完,剩下的玫瑰花做垃圾处理。
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式。
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
|
日需求量n |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
频数 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
【命题意图】本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率,是简单题.
【解析】(Ⅰ)当日需求量 时,利润
时,利润 =85;
=85;
当日需求量 时,利润
时,利润 ,
,
∴ 关于
关于 的解析式为
的解析式为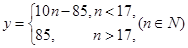 ;
;
(Ⅱ)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的平均利润为
 =76.4;
=76.4;
(ii)利润不低于75元当且仅当日需求不少于16枝,故当天的利润不少于75元的概率为

设抛物线 :
: (
( >0)的焦点为
>0)的焦点为 ,准线为
,准线为 ,
, 为
为 上一点,已知以
上一点,已知以 为圆心,
为圆心, 为半径的圆
为半径的圆 交
交 于
于 ,
, 两点.
两点.
(Ⅰ)若 ,
, 的面积为
的面积为 ,求
,求 的值及圆
的值及圆 的方程;
的方程;
(Ⅱ)若 ,
, ,
, 三点在同一条直线
三点在同一条直线 上,直线
上,直线 与
与 平行,且
平行,且 与
与 只有一个公共点,求坐标原点到
只有一个公共点,求坐标原点到 ,
, 距离的比值.
距离的比值.
【命题意图】本题主要考查圆的方程、抛物线的定义、直线与抛物线的位置关系、点到直线距离公式、线线平行等基础知识,考查数形结合思想和运算求解能力.
【解析】设准线 于
于 轴的焦点为E,圆F的半径为
轴的焦点为E,圆F的半径为 ,
,

则|FE|= ,
, =
= ,E是BD的中点,
,E是BD的中点,
(Ⅰ) ∵ ,∴
,∴ =
= ,|BD|=
,|BD|= ,
,
设A( ,
, ),根据抛物线定义得,|FA|=
),根据抛物线定义得,|FA|= ,
,
∵ 的面积为
的面积为 ,∴
,∴ =
= =
= =
= ,解得
,解得 =2,
=2,
∴F(0,1), FA|= , ∴圆F的方程为:
, ∴圆F的方程为: ;
;
(Ⅱ) 解析1∵ ,
, ,
, 三点在同一条直线
三点在同一条直线 上, ∴
上, ∴ 是圆
是圆 的直径,
的直径, ,
,
由抛物线定义知 ,∴
,∴ ,∴
,∴ 的斜率为
的斜率为 或-
或- ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
设直线 的方程为:
的方程为: ,代入
,代入 得,
得, ,
,
∵ 与
与 只有一个公共点,
∴
只有一个公共点,
∴ =
= ,∴
,∴ ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
∴坐标原点到 ,
, 距离的比值为3.
距离的比值为3.
解析2由对称性设 ,则
,则
点 关于点
关于点 对称得:
对称得:
得: ,直线
,直线
 切点
切点
直线
坐标原点到 距离的比值为
距离的比值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com