
题目列表(包括答案和解析)
(14分)已知椭圆![]() 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C![]() 上任一点,MN是圆
上任一点,MN是圆![]() 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为![]() 的直线
的直线![]() 恰好与圆
恰好与圆![]() 相切。
相切。
(1)已知椭圆![]() 的离心率;
的离心率;
(2)若![]() 的最大值为49,求椭圆C
的最大值为49,求椭圆C![]() 的方程。
的方程。
已知椭圆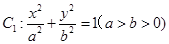 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C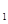 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线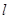 恰好与圆
恰好与圆 相切.
相切.
(Ⅰ)已知椭圆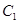 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.(本题12分)
已知椭圆 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆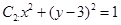 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切.
(Ⅰ)求椭圆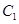 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
(本题12分)
已知椭圆 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线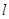 恰好与圆
恰好与圆 相切.
相切.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
一、选择题:每小题5分,共60分
BCCAB ACADB BB
二、填空题:每小题4分,共16分
13. ,甲,甲:
,甲,甲: ①
①
三、解答题:本题满分共74分,解答应有必要的文字说明,解答过程或演算步骤
17.解:(1)甲、乙二人抽到的牌的所有基本事件(放快4用
(2)甲抽到3,乙抽到的牌只能是2,4,
因此乙抽到的牌的数字大于3的概率是 ;------------------------(6分)
;------------------------(6分)
(3)甲抽到牌比乙大有(3,2),(4,2),(4,3),( ,乙获胜的与甲获胜是对立事件,所以乙获胜的概率是
,乙获胜的与甲获胜是对立事件,所以乙获胜的概率是 ,
,
 此游戏不公平------------------(12分)
此游戏不公平------------------(12分)
18.解:(1)由题意知 .
.

 (5分)
(5分)
 ,
,
 -----------------(7分)
-----------------(7分)
(2)


 -------------------------------------(9分)
-------------------------------------(9分)

 ---------------(12分)
---------------(12分)
19.解:(1) 低面ABCD是正方形,O为中心,
低面ABCD是正方形,O为中心, AC⊥BD
AC⊥BD
又SA=SC, AC⊥SO,又SO
AC⊥SO,又SO BD=0,
BD=0, AC⊥平面SBD-----------------(6分)
AC⊥平面SBD-----------------(6分)
 (2)连接
(2)连接


又由(1)知,AC⊥BD
且AC⊥平面SBD,
所以,AC⊥SB---------------(8分)
 ⊥
⊥
 ⊥
⊥ ,且EM
,且EM NE=E
NE=E
 ⊥平面EMN-------------(10分)
⊥平面EMN-------------(10分)
因此,当P点在线段MN上移动时,总有AC⊥EP-----(12分)
20.解:
 -------------------------------(2分)
-------------------------------(2分)
(2)
则
令 --------------------------------(4分)
--------------------------------(4分)
当x在区间[-1,2]上变化时,y’,y的变化情况如下表:
X
-1



1
(1,2)
2
Y’
+
0
-
0
+
Y
3/2
单增
极大值
单减
极小值
单增
3
又


 -----------(6分)
-----------(6分)
(3)证明:
又


 ---------------------(12分)
---------------------(12分)
21.解:(1)
当
当 ,适合上式,
,适合上式,
 -------------------------------(4分)
-------------------------------(4分)
(2) ,
,
 ①
①
 , ②
, ②
两式相减,得

=
=
=
 --------------------------------(8分)
--------------------------------(8分)
(3)证明,由

又

=
 成立---------------------------------------------------(12分)
成立---------------------------------------------------(12分)
22.解:(1)由题意可知直线l的方程为 ,
,
因为直线与圆 相切,所以
相切,所以 =1,既
=1,既
从而 ----------------------------------------------------------------------------------------(6分)
----------------------------------------------------------------------------------------(6分)
(2)设 则
则

 ---------------------------------(8分)
---------------------------------(8分)
j当

k当
 故舍去。
故舍去。
综上所述,椭圆的方程为 ------------------------------------(14分)
------------------------------------(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com