
题目列表(包括答案和解析)
 p是
p是 q的必要不充分条件;
q的必要不充分条件;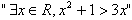 的否定是
的否定是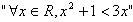 ;
;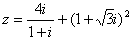 ,则z=
,则z=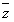 。
。给出下列四个结论:
①在画两个变量的散点图时,预报变量在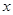 轴上,解释变量在
轴上,解释变量在 轴上;
轴上;
②线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越小;
③用独立性检验(2Χ2列联表法)来考察两个分类变量是否有关系时,算出的随机变量k2的值越大,说明“x与y有关系”成立的可能性越大;
④残差平方和越小的模型,拟合的效果越好;
其中结论正确的序号为 。(写出你认为正确的所有结论的序号)
某工厂![]() 年来生产某种产品的总产量
年来生产某种产品的总产量![]() 与时间
与时间![]() (年)的函数关系如图所示,有下列四种说法:①前三年中产量增长的速度越来越快;②前三年中产量增长的速度越来越慢;③前三年中年产量保持不变;④第三年后,这种产品停止生产。其中正确的说法是 (只要写出说法的序号)
(年)的函数关系如图所示,有下列四种说法:①前三年中产量增长的速度越来越快;②前三年中产量增长的速度越来越慢;③前三年中年产量保持不变;④第三年后,这种产品停止生产。其中正确的说法是 (只要写出说法的序号)
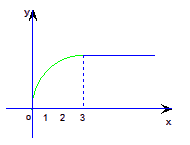
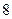 年来生产某种产品的总产量
年来生产某种产品的总产量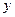 与时间
与时间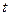 (年)的函数关系如图所示,有下列四种说法:①前三年中产量增长的速度越来越快;②前三年中产量增长的速度越来越慢;③前三年中年产量保持不变;④第三年后,这种产品停止生产。其中正确的说法是 (只要写出说法的序号)
(年)的函数关系如图所示,有下列四种说法:①前三年中产量增长的速度越来越快;②前三年中产量增长的速度越来越慢;③前三年中年产量保持不变;④第三年后,这种产品停止生产。其中正确的说法是 (只要写出说法的序号) 
(08年聊城市一模) 给出以下命题:
①合情推理是由特殊到一般的推理,得到的结论不一定正确,演绎推是由一般到特殊的推理,得到的结论一定正确。
②甲、乙两同学各自独立地考察两个变量X、Y的线性相关关系时,发现两人对X的观察数据的平均值相等,都是s,对Y的观察数据的平均值也相等,都是t,各自求出的回归直线分别是l1、l2,则直线l1与l2必定相交于点(s,t)。
③某企业有职工150人,其中高级职称15人,中级职称45人,一般职员90人,若用分层抽样的方法抽出一个容量为30的样本,则一般职员应抽出20人。
④用独立性检验(2×2列联表法)来考察两个分类变量是否有关系时,算出的随机变量K2的值越大,说明“X与Y有关系”成立的可能性越大。
其中真命题的序号是 (写出所有真命题的序号)。
一、选择题:本大题共12个小题,每小题5分,共60分。
1―6BBCDBD 7―12CACAAC
二、填空题:本大题共4个小题,每小题4分,共16分。
13.0.8;
14.
15. ;
;
16.①③
三、解答题:
17.解:(1)由 ,
,
得

由正弦定得,得

又B

又
又 6分
6分
(2)
由已知
 9分
9分
当
因此,当 时,
时,

当 ,
,
 12分
12分
18.解:(1)依题意,甲答对主式题数 的可能取值为0,1,2,3,则
的可能取值为0,1,2,3,则



 4分
4分
 的分布列为
的分布列为

0
1
2
3
P




甲答对试题数 的数学期望为
的数学期望为
 6分
6分
(2)设甲、乙两人考试合格的事件分别为A、B,则

 9分
9分
因为事件A、B相互独立,
 甲、乙两人考试均不合格的概率为
甲、乙两人考试均不合格的概率为

 甲、乙两人至少有一人考试合格的概率为
甲、乙两人至少有一人考试合格的概率为

答:甲、乙两人于少有一人考试合格的概率为 12分
12分
另解:甲、乙两人至少有一个考试合格的概率为

答:甲、乙两人于少有一人考试合格的概率为
19.解法一(1)过点E作EG 交CF于G,
交CF于G,
|