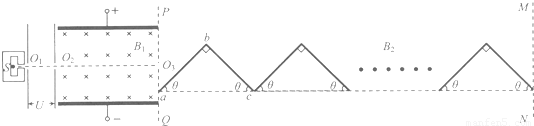
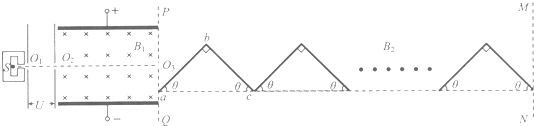
如图所示，粒子源S可以不断地产生质量为m、电荷量为+q的粒子，粒子从小孔O₁漂进（不计初速）一个水平方向的加速电场，再经小孔0₂进入相互正交的匀强电场和匀强磁场区域，其电场强度大小为E，磁感应强度大小为B₁，方向如图．虚线PQ、MN之间存在着水平向右的匀强磁场，磁感应强度大小为B₂（方向图中未画出）．现有n块折成直角的相同硬质塑料板abc（不带电，宽度很窄，厚度不计）紧靠在一起，恰好放置在PQ、MN之间（截面图如图），ab=bc=L，θ=45°．现使粒子能沿水平虚线0₂0₃进入PQ、MN之间的区域．假设粒子的重力、空气阻力均不计，粒子与板相碰后，速率不变，方向变化遵守光的反射定律．求：



（1）加速电压U
（2）粒子在B₂磁场中运动的总时间t；
（3）粒子在PQ、MN之间运动的平均速度大小v，．

在高能物理研究中，粒子加速器起着重要作用，而早期的加速器只能使带电粒子在高压电场中加速一次，因而粒子所能达到的能量受到高压技术的限制．1930年，Earnest O．Lawrence博士提出了回旋加速器的理论，他设想用磁场使带电粒子沿圆弧形轨道旋转，多次反复地通过高频加速电场，直至达到高能量，图甲为他设计的回旋加速器的示意图．它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条狭缝，两个D型盒处在匀强磁场中并接有高频交变电压．图乙为俯视图，在D型盒上半面中心S处有一正离子源，它发出的正离子，经狭缝电压加速后，进入D型盒中，在磁场力作用下运动半周，再经狭缝电压加速；为保证粒子每次经过狭缝都被加速，应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致．如此周而复始，最后到达D型盒的边缘，获得最大速度后被束流提取装置提取．设被加速的粒子为质子，质子的电荷量为q，质量为m，加速时电极间电压大小恒为U，磁场的磁感应强度为B，D型盒的半径为R，狭缝之间的距离为d，质子从离子源出发时的初速度为零，分析时不考虑相对论效应．

（1）求质子经第1次加速后进入一个D形盒中的回旋半径与第2次加速后进入另一个D形盒后的回旋半径之比；
（2）若考虑质子在狭缝中的运动时间，求质子从离开离子源到被第n次加速结束时所经历的时间；
（3）若要提高质子被此回旋加速器加速后的最大动能，可采取什么措施？
（4）若使用此回旋加速器加速氘核，要想使氘核获得与质子相同的最大动能，请你通过分析，提出一个简单可行的办法．

在高能物理研究中，粒子加速器起着重要作用，而早期的加速器只能使带电粒子在高压电场中加速一次，因而粒子所能达到的能量受到高压技术的限制．1930年，Earnest O．Lawrence博士提出了回旋加速器的理论，他设想用磁场使带电粒子沿圆弧形轨道旋转，多次反复地通过高频加速电场，直至达到高能量，图甲为他设计的回旋加速器的示意图．它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条狭缝，两个D型盒处在匀强磁场中并接有高频交变电压．图乙为俯视图，在D型盒上半面中心S处有一正离子源，它发出的正离子，经狭缝电压加速后，进入D型盒中，在磁场力作用下运动半周，再经狭缝电压加速；为保证粒子每次经过狭缝都被加速，应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致．如此周而复始，最后到达D型盒的边缘，获得最大速度后被束流提取装置提取．设被加速的粒子为质子，质子的电荷量为q，质量为m，加速时电极间电压大小恒为U，磁场的磁感应强度为B，D型盒的半径为R，狭缝之间的距离为d，质子从离子源出发时的初速度为零，分析时不考虑相对论效应．



（1）求质子经第1次加速后进入一个D形盒中的回旋半径与第2次加速后进入另一个D形盒后的回旋半径之比；
（2）若考虑质子在狭缝中的运动时间，求质子从离开离子源到被第n次加速结束时所经历的时间；
（3）若要提高质子被此回旋加速器加速后的最大动能，可采取什么措施？
（4）若使用此回旋加速器加速氘核，要想使氘核获得与质子相同的最大动能，请你通过分析，提出一个简单可行的办法．

在高能物理研究中，粒子加速器起着重要作用，而早期的加速器只能使带电粒子在高压电场中加速一次，因而粒子所能达到的能量受到高压技术的限制。1930年，Earnest O. Lawrence提出了回旋加速器的理论，他设想用磁场使带电粒子沿圆弧形轨道旋转，多次反复地通过高频加速电场，直至达到高能量。图甲为Earnest O. Lawrence设计的回旋加速器的示意图。它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条狭缝；两个D型盒处在匀强磁场中并接有高频交变电压。图乙为俯视图，在D型盒上半面中心S处有一正离子源，它发出的正离子，经狭缝电压加速后，进入D型盒中。在磁场力的作用下运动半周，再经狭缝电压加速；为保证粒子每次经过狭缝都被加速，应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致。如此周而复始，最后到达D型盒的边缘，获得最大速度后被束流提取装置提取出。已知正离子的电荷量为q，质量为m，加速时电极间电压大小恒为U，磁场的磁感应强度为B，D型盒的半径为R，狭缝之间的距离为d。设正离子从离子源出发时的初速度为零。
（1）试计算上述正离子从离子源出发被第一次加速后进入下半盒中运动的轨道半径；
（2）尽管粒子在狭缝中每次加速的时间很短但也不可忽略。试计算上述正离子在某次加速过程当中从离开离子源到被第n次加速结束时所经历的时间；
（3）不考虑相对论效应，试分析要提高某一离子被半径为R的回旋加速器加速后的最大动能可采用的措施。