
题目列表(包括答案和解析)
已知定义在R上的单调递增函数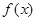 满足
满足 ,且
,且 。
。
(Ⅰ)判断函数 的奇偶性并证明之;
的奇偶性并证明之;
(Ⅱ)解关于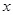 的不等式:
的不等式: ;
;
(Ⅲ)设集合 ,
, .
. ,若集合
,若集合 有且仅有一个元素,求证:
有且仅有一个元素,求证:  。
。
已知定义在R上的单调递增函数 满足
满足 ,且
,且 。
。
(Ⅰ)判断函数 的奇偶性并证明之;
的奇偶性并证明之;
(Ⅱ)解关于 的不等式:
的不等式: ;
;
(Ⅲ)设集合 ,
, .
. ,若集合
,若集合 有且仅有一个元素,求证:
有且仅有一个元素,求证:  。
。
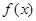 满足
满足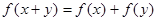 ,且
,且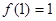 。
。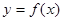 的奇偶性并证明之;
的奇偶性并证明之;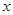 的不等式:
的不等式: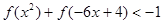 ;
;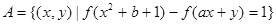 ,
,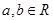 .
.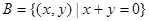 ,若集合
,若集合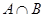 有且仅有一个元素,求证:
有且仅有一个元素,求证: 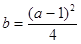 。
。 已知函数f(x)=x3-ax-1.
(1)若f(x)在实数集R上单调递增,求实数a的取值范围;
(2)是否存在实数a,使f(x)在(-1,1)上单调递减?若存在,求出a的取值范围;若不存在,说明理由;
(3)证明:f(x)=x3-ax-1的图象不可能总在直线y=a的上方.
一、选择题:本大题共10个小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
B
A
D
B
A
二、填空题:本大题共4个小题,每小题4分,共16分.
11. 630 12. 2k 13.  14. ①②③
14. ①②③
三、解答题:本大题共6个小题,每小题14分,共84分.
15. (4分)
(4分) 
由题意得

16.  有分布列:
有分布列:

0
1
2
3
P




从而期望
17.(1)
又

(2) 


(3)DE//AB,
(4)设BB1的中点为F,连接EF、DF,则EF是DF在平面BB
因为BB

18.(1) 由题意得

(2) 
所以直线 的斜率为
的斜率为
令 ,则直线
,则直线 的斜率
的斜率 ,
,
19.(1)由韦达定理得


 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
(2)由(1)知 ,则
,则
原式左边=
= =右式。故原式成立。
=右式。故原式成立。
20.令x=y=0,有 ,令y=-x则
,令y=-x则 得
得
故(1)得证。
(2)在R上任取x1,x2且 ,且
,且 ,
,

所以 在R上单调递增;
在R上单调递增;
(3)
由
 得
得 ;
;
由 得
得 ;因为
;因为 ,
,
所以 无解,即圆心到直线的距离大于或等于半径2,只需
无解,即圆心到直线的距离大于或等于半径2,只需

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com