
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在函数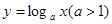 的图象上有
的图象上有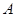 、
、 、
、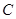 三点,横坐标分别为
三点,横坐标分别为 其中
其中 .
.
⑴求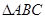 的面积
的面积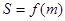 的表达式;
的表达式;
⑵求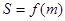 的值域.
的值域.
【解析】由题意利用分割可先表示三角形ABC的面积,然后应用对数运算性质及二次函数的性质求解函数的最大值,属于知识的简单综合.
| 9 | 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com