
题目列表(包括答案和解析)
(本小题满分12分)
PM2. 5是指大气中直径小于或等于2. 5微米的颗粒物,也称为 可人肺颗粒物.我国PM2. 5标准采用世卫组织设定的最宽限 值,即PM2.5日均值在35微克/立方米以下空气质量为一级; 在35微克/立方米~75微克/立方米之间空气质量为二级;在 75微克/立方米以上空气质量为超标.
某市环保局从市区2012年全年每天的PM2.5监测数据中 随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为 茎,个位为叶)

(I)从这9天的数据中任取2天的数据,求恰有一天空气质量达到一级的概率;
(II) 以这9天的PM2. 5日均值来估计供暖期间的空气质量情况,则供暖期间(按150天计算)中大约有多少天的空气质量达到一级.
(本小题满分12分)
PM2. 5是指大气中直径小于或等于2. 5微米的颗粒物,也称为 可人肺颗粒物.我国PM2. 5标准采用世卫组织设定的最宽限 值,即PM2.5日均值在35微克/立方米以下空气质量为一级; 在35微克/立方米~75微克/立方米之间空气质量为二级;在 75微克/立方米以上空气质量为超标.
某市环保局从市区2012年全年每天的PM2.5监测数据中 随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为 茎,个位为叶)
(I)从这9天的数据中任取2天的数据,求恰有一天空气质量达到一级的概率;
(II) 以这9天的PM2. 5日均值来估计供暖期间的空气质量情况,则供暖期间(按150天计算)中大约有多少天的空气质量达到一级.
(本小题满分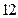 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望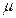 及标准差
及标准差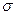 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在 范围中的学生的人数.
范围中的学生的人数.
(Ⅲ) 如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| | 身高达标 | 身高不达标 | 总计 |
| 积极参加体育锻炼 | 40 | | |
| 不积极参加体育锻炼 | | 15 | |
| 总计 | | | 100 |
 =
=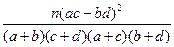 ,参考数据:
,参考数据:P(K  k) k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(本小题满分13分)2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
|
组别 |
PM2.5(微克/立方米) |
频数(天) |
频 率 |
|
第一组 |
(0,15] |
4 |
0.1 |
|
第二组 |
(15,30] |
12 |
|
|
第三组 |
(30,45] |
8 |
0.2 |
|
第四组 |
(45,60] |
8 |
0.2 |
|
第五组 |
(60,75] |
|
0.1 |
|
第六组 |
(75,90) |
4 |
0.1 |
(Ⅰ)试确定 的值,并写出该样本的众数和中位数(不必写出计算过程);
的值,并写出该样本的众数和中位数(不必写出计算过程);
(Ⅱ)完成相应的频率分布直方图.
(Ⅲ)求出样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.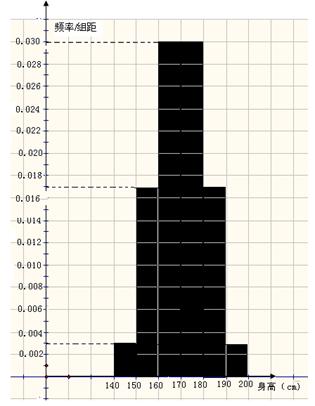
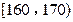 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望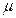 及标准差
及标准差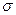 (精确到0.1);
(精确到0.1);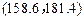 范围中的学生的人数.
范围中的学生的人数.| | 身高达标 | 身高不达标 | 总计 |
| 积极参加体育锻炼 | 40 | | |
| 不积极参加体育锻炼 | | 15 | |
| 总计 | | | 100 |
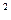 =
=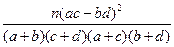 ,参考数据:
,参考数据:P(K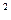 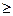 k) k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com