17.已知:函数. (1)求:函数的定义域, (2)判断函数的奇偶性并说明理由, (3)判断函数在()上的单调性.并用定义加以证明. 卷(II) 一.选择题:(本大题共3小题.每小题4分.共12分) 1.函数中.若.则( ) A. B. C. D.4 2.如果函数是奇函数.那么( ) A.1 B.2 C.-1 D.-2 3.设P.Q为两个非空实数集.定义集合.若..则中元素的个数是( ) A.6 B.7 C.8 D.9 二.填空题:(本大题共2小题.每小题4分.共8分) 4. . 5.如果函数在区间[1.2]上是减函数.那么实数的取值范围是 ,如果函数与函数在区间[1.2]上都是减函数.那么实数的取值范围是 . 三.解答题:(本大题共3小题.满分共30分) 6.求:函数的最值及取得最值时的值. 【
查看更多】
题目列表(包括答案和解析)
函数
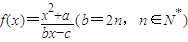
的定义域为{x|x≠1},图象过原点,且
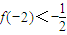
.
(1)试求函数f(x)的单调减区间;
(2)已知各项均为负数的数列{a
n}前n项和为S
n,满足

,求证:

;
(3)设

,是否存在m
1,,n
1,m
2,n
2∈N*,使得ln2011∈(g(m
1,n
1),g(m
2,n
2))?若存在,求出m
1,,n
1,m
2,n
2,证明结论;若不存在,说明理由.
查看答案和解析>>
函数

的定义域为{x|x≠1},图象过原点,且

.
(1)试求函数f(x)的单调减区间;
(2)已知各项均为负数的数列{a
n}前n项和为S
n,满足

,求证:

.
查看答案和解析>>
函数

的定义域为{x|x≠1},图象过原点,且
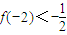
.
(1)试求函数f(x)的单调减区间;
(2)已知各项均为负数的数列{a
n}前n项和为S
n,满足

,求证:

;
(3)设

,是否存在m
1,,n
1,m
2,n
2∈N*,使得ln2011∈(g(m
1,n
1),g(m
2,n
2))?若存在,求出m
1,,n
1,m
2,n
2,证明结论;若不存在,说明理由.
查看答案和解析>>
函数

的定义域为{x|x≠1},图象过原点,且

.
(1)试求函数f(x)的单调减区间;
(2)已知各项均为负数的数列{a
n}前n项和为S
n,满足

,求证:

;
(3)设

,是否存在m
1,,n
1,m
2,n
2∈N*,使得ln2011∈(g(m
1,n
1),g(m
2,n
2))?若存在,求出m
1,,n
1,m
2,n
2,证明结论;若不存在,说明理由.
查看答案和解析>>
已知:函数 ,
,
(1)求:函数f(x)的定义域;判断函数f(x)的奇偶性并说明理由;
(2)判断函数f(x)在(0,+∞)上的单调性,并用定义加以证明.
查看答案和解析>>

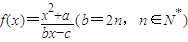 的定义域为{x|x≠1},图象过原点,且
的定义域为{x|x≠1},图象过原点,且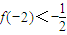 .
. ,求证:
,求证: ;
; ,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由.
,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由. 的定义域为{x|x≠1},图象过原点,且
的定义域为{x|x≠1},图象过原点,且 .
. ,求证:
,求证: .
. 的定义域为{x|x≠1},图象过原点,且
的定义域为{x|x≠1},图象过原点,且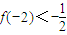 .
. ,求证:
,求证: ;
; ,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由.
,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由. 的定义域为{x|x≠1},图象过原点,且
的定义域为{x|x≠1},图象过原点,且 .
. ,求证:
,求证: ;
; ,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由.
,是否存在m1,,n1,m2,n2∈N*,使得ln2011∈(g(m1,n1),g(m2,n2))?若存在,求出m1,,n1,m2,n2,证明结论;若不存在,说明理由. ,
,