
题目列表(包括答案和解析)
对于一个有n项的数列P=(p1,p2,…,pn),P的“蔡查罗和”定义为s1、s2、…sn、的算术平均值,其中sk=p1+p2+…pk(1≤k≤n),若数列(p1,p2,…,p2006)的“蔡查罗和”为2007,那么数列(1,p1,p2,…,p2006)的“蔡查罗和”为 ( )
A.2007 B.2008 C.2006 D.1004
| 1 | n |
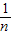 (S1+S2+…+Sn)其中Sk=(P1+P2+…+Pn)(1≤k≤n)若一个100项的数列(P1,P2,…,P100)的“蔡查罗和”为201.97,那么102项数列(1,1,P1,P2,…,P100)的“蔡查罗和”为 .
(S1+S2+…+Sn)其中Sk=(P1+P2+…+Pn)(1≤k≤n)若一个100项的数列(P1,P2,…,P100)的“蔡查罗和”为201.97,那么102项数列(1,1,P1,P2,…,P100)的“蔡查罗和”为 .对于一个有限数列P={P1,P2,……Pn},P的蔡查罗和(蔡查罗为一数学家)定义为![]() (S1+S2+…+Sn),其中SK=P1+P2+……+PK(1≤K≤n),若一个99项的数列{P1,P2,……P99}的蔡查罗和为1000,则100项数列{1,P1,P2,……P99}的蔡查罗和为________.
(S1+S2+…+Sn),其中SK=P1+P2+……+PK(1≤K≤n),若一个99项的数列{P1,P2,……P99}的蔡查罗和为1000,则100项数列{1,P1,P2,……P99}的蔡查罗和为________.
已知数列{an}有a1=a,a2=p(常数p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足![]() .
.
(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)对于数列{bn},假如存在一个常数b使得对任意的正整数n都有bn<b,且![]() ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令![]() ,求数列{p1+p2+…+pn-2n}的“上渐近值”.
,求数列{p1+p2+…+pn-2n}的“上渐近值”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com