
题目列表(包括答案和解析)
已知半径为1的定圆⊙P的圆心P到定直线![]() 的距离为2,Q是
的距离为2,Q是![]() 上一动点,⊙Q与⊙P相外切,⊙Q交
上一动点,⊙Q与⊙P相外切,⊙Q交![]() 于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。
于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。
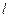 的距离为2,Q是
的距离为2,Q是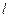 上一动点,⊙Q与⊙P相外切,⊙Q交
上一动点,⊙Q与⊙P相外切,⊙Q交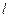 于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。
于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。 一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| 3 |
已知圆C以![]() 为圆心,5为半径,过点S
为圆心,5为半径,过点S![]() 作直线
作直线![]() 与圆C交于A,B两点.
与圆C交于A,B两点.
(1)若AB=8,求直线![]() 的方程;
的方程;
(2)当直线![]() 的斜率为
的斜率为![]() 时,在
时,在![]() 上求一点P,使P到圆C的切线长等于PS;
上求一点P,使P到圆C的切线长等于PS;
(3)设AB的中点为N,试在平面上找一定点M,使MN的长为定值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com