
题目列表(包括答案和解析)
(2007
·山东潍坊)如下图,已知A、B、C是椭圆E: 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为 ,BC过椭圆中心O,且AC⊥BC,
,BC过椭圆中心O,且AC⊥BC, .求点C的坐标及椭圆E的方程.
.求点C的坐标及椭圆E的方程.

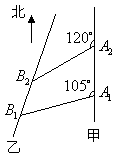
(2007山东理20)如图,甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于![]() 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,当甲船航行
海里,当甲船航行![]() 分钟到达
分钟到达![]() 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
(2007
山东,8)某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;……第六组,成绩大于等于18秒且小于等于19秒.如图所示是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为
[
]|
A .0.9,35 |
B .0.9,45 |
C .0.1,35 |
D .0.1,45 |
(2007
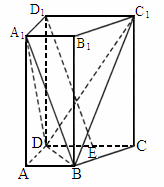
山东,19)如下图,在直四棱柱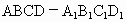 中,已知
中,已知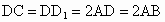 ,AD⊥DC,AB∥DC.
,AD⊥DC,AB∥DC.
(1)
设E是DC的中点,求证: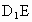 ∥平面
∥平面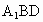 ;
;
(2)
求二面角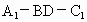 的余弦值.
的余弦值.
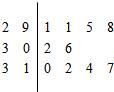 如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( )
如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( )| A、304.6 | B、303.6 | C、302.6 | D、301.6 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com