练习册

  • 练习册
  • 试题
    2006―2007学年度第一学期 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•石景山区二模）北京市2001-2010年星级饭店客房出租率（%）的情况如下表：
    年份 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010
    出租率 62 62 52 65 62 61 60 52 49 56
    表中出租率（%）的中位数和众数分别为（　　）

    查看答案和解析>>

    观察下列各式
    		1+1×2×3×4
    =1×(1+3)+1
    		1+2×3×4×5
    =2×(2+3)+1
    		1+3×4×5×6
    =3×(3+3)+1
    根据以上规律，直接写出结果
    		1+2006×2007×2008×2009
    =
     
    ．

    查看答案和解析>>

    23、几年来，岳阳经济快速发展，居民收入不断提高．根据统计部门统计，绘制了2005年～2009年岳阳市居民人均纯收入和农村居民人均纯收入的条形统计图（如图①）．农村居民人均纯收入占全市居民人均纯收入的大致比例统计表（单位：元）
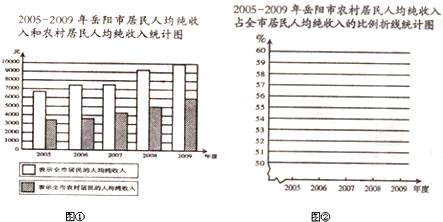
    年   度 2005 2006 2007 2008 2009
    全市居民人均纯收入 6900 7416 7800 9090
    全市农村居民人均纯收入 3657 3876 4134 6000
    农村居民人均纯收入占全
    市居民人均纯收入的比例    		 53% 52.3% 53%
    （1）请你根据图①提供的信息将上表补充完整；
    （2）请在图②中，将年度农村居民人均纯收入占全市居民人均纯收入的比例，绘制成折线统计图．

    查看答案和解析>>

    在数1、2、3、4、…、2009、2010的每个数字前添上“+”或“-”，使得算出的结果是一个最小的非负数，请写出符合条件的式子：
    1-2+3-4+5-6+7-8+…+2006-2007+2008-2009+2010
    1-2+3-4+5-6+7-8+…+2006-2007+2008-2009+2010
    ．

    查看答案和解析>>

    某厂从2005年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：
    年    度 2006 2007 2008 2009
    投入技改资金x（万元） 2.5 3 4 4.5
    产品成本y（万元/件） 7.2 6 4.5 4
    （1）请你认真分析表中数据，从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律，说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
    （2）按照这种变化规律，若2010年已投入技改资金5万元．
    ①预计生产成本每件比2009年降低多少万元？
    ②如果打算在2009年把每件产品成本降低到3.2万元，则还需投入技改资金多少万元？（结果精确到0.01万元）

    查看答案和解析>>

    一、BACBB   CDCCA

    二、11．答案不唯一，如：，π，0.1010010001…      12.     

    13．3,90   14. 2    15．15   16．菱形   17．24     18. 60°

    三、19．(m)

    20.（1）原式=  ………………………………………… 2分

                =               ………………………………………… 3分

    当时，

    原式=   ………………………………… 4分

    =1-1+4

    =4.                         ………………………………………… 5分

    （2）原式=   …………………………………… 1分

    =            ………………………………………… 2分

    =                        ………………………………………… 3分

    当时，

    原式=                  ………………………………………… 4分

    =.                       ………………………………………… 5分

    21.（1）原式=3(a2-8a+16)                 ………………………………………… 2分

    =3(a-4)2.                    ………………………………………… 5分

       （2）原式=m2+m-4m-4+3m                ………………………………………… 2分

                =m2-4                        ………………………………………… 3分

                =(m+2)(m-2).                 ………………………………………… 5分

    22. 正确画△A1B1C1给3分，正确画△A2B2C2给3分，共6分.

     

    23. 在ABCD中，AB=DC，AD=BC.         ………………………………………… 2分

    ∴ AB+AD=.               ………………………………………… 3分

    ∵ AD=2AD,

    ∴ 2AD+AD=12.                      ………………………………………… 4分

    ∴ AD=4，BC=4.                     ………………………………………… 6分

       AB=DC=8.                        ………………………………………… 7分

    24. △OAB是等边三角形的理如下：

    在矩形ABCD中，OA=0C，OB=OD,       ………………………………………… 2分

    AC=BD,                             ………………………………………… 4分

    ∴ OA=AC，OB=BD.               ………………………………………… 6分

    又∵ AB=AC，                      

    ∴ OA=OB=AB.

    即△OAB是等边三角形.               ………………………………………… 7分

    25. （1）在ABCD中，∠DAB+∠ABC=180°，………………………………………… 2分

             ∵ AE，BF分别平分∠DAB和∠ABC，

             ∴ ∠EAB+∠FBA=90°，           ………………………………………… 3分

             ∴ AE⊥BF.                      ………………………………………… 4分

        （2）在ABCD中，DA=CB，DC∥AB,     ………………………………………… 6分

             ∴ ∠EAB=∠DEA，                ………………………………………… 7分

             ∵ ∠DAE=∠EAB，

             ∴ ∠DAE=∠DEA，                ………………………………………… 8分

             ∴DA=DE.                        ………………………………………… 9分

             同理，得 CF=CB.                 ………………………………………… 10分

             ∴ DE=CF,                       ………………………………………… 11分

             ∴ DE-FE=CF-FE,

             即 DF=CF.                       ………………………………………… 12分

     

     

     

     

     


    同步练习册答案