平面向量与三角函数的交汇是近年来的考查热点.一般服出现在解答题的前三大题里.在复习中.应加强这种类型试题的训练. [母题特供]每个专题5道最典型试题 母题一: 金题引路: 已知:向量(1)若点能构成三角形.求出实数应满足的条件,(2)若为直角三角形.且为直角.求实数的值. 解:(1)要使点能构成三角形.只要三点不共线. 由有: 所以只要即 (2)因为为直角三角形.且为直角 符合题意. 母题二: 金题引路: 已知向量(Ⅰ)当时.求函数的值域,(Ⅱ)若的值. 解:(Ⅰ)由 ∵∴的值域为[-1.2] (Ⅱ)∵∴∴ ∴ 母题三: 金题引路: 设函数.其中向量. (1)求函数的最小正周期 (Ⅰ)求函数f(x)的单调递减区间,(Ⅱ)求函数f(x)的最大值及取得最大值时的x的取值集合. 解:(Ⅰ)f(x)=×= (2cosx+1,cos2x-sinx+1)×(cosx,-1)=2cos2x+cosx-cos2x+sinx-1 =cosx+sinx =sin(x+) 令2kp+£x+£2kp+.kÎZ 解得:2kp+£x£2kp+所以.函数f(x)的单调递减区间[2kp+,2kp+].kÎZ (Ⅱ)函数f(x)的最大值是.此时x+=2kp+.即x=2kp+ ∴函数f(x)取得最大值时.x的取值集合为{x|x=2kp+.kÎZ} 母题五.金题引路: 如图4.已知点和单位圆上半部分上的动点. ⑴若.求向量, ⑵求的最大值. 【
查看更多】
题目列表(包括答案和解析)
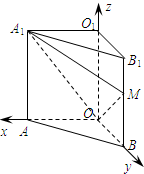
(2009•闵行区一模)如图,直三棱柱OAB-O
1A
1B
1中,∠AOB=90°,M是侧棱BB
1上一点,向量
=(1, 1, -1)是平面OA
1M的一个法向量,则平面OAB与平面OA
1M所成二面角的锐角为
(结果用反三角函数值表示).
查看答案和解析>>
设
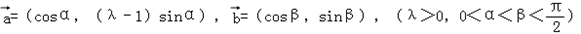
是平面上的两个向量,若向量
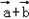
与
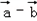
相互垂直,
(1)求实数λ的值;
(2)若
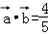
,且
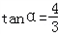
,求α的值(结果用反三角函数值表示)
查看答案和解析>>
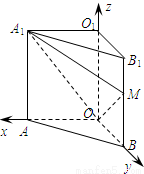
如图,直三棱柱OAB-O
1A
1B
1中,∠AOB=90°,M是侧棱BB
1上一点,向量
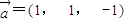
是平面OA
1M的一个法向量,则平面OAB与平面OA
1M所成二面角的锐角为
(结果用反三角函数值表示).
查看答案和解析>>
(理)设
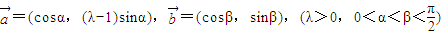
是平面上的两个向量,若向量
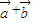
与
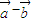
相互垂直,
(1)求实数λ的值;
(2)若
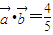
,且
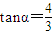
,求α的值(结果用反三角函数值表示)
查看答案和解析>>
(理)设
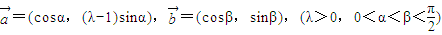
是平面上的两个向量,若向量
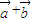
与
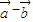
相互垂直,
(1)求实数λ的值;
(2)若
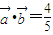
,且
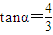
,求α的值(结果用反三角函数值表示)
查看答案和解析>>

 (2009•闵行区一模)如图,直三棱柱OAB-O1A1B1中,∠AOB=90°,M是侧棱BB1上一点,向量
(2009•闵行区一模)如图,直三棱柱OAB-O1A1B1中,∠AOB=90°,M是侧棱BB1上一点,向量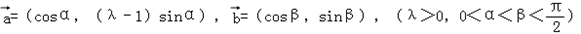 是平面上的两个向量,若向量
是平面上的两个向量,若向量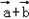 与
与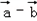 相互垂直,
相互垂直,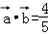 ,且
,且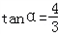 ,求α的值(结果用反三角函数值表示)
,求α的值(结果用反三角函数值表示)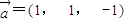 是平面OA1M的一个法向量,则平面OAB与平面OA1M所成二面角的锐角为 (结果用反三角函数值表示).
是平面OA1M的一个法向量,则平面OAB与平面OA1M所成二面角的锐角为 (结果用反三角函数值表示).
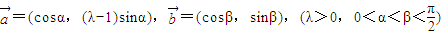 是平面上的两个向量,若向量
是平面上的两个向量,若向量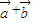 与
与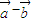 相互垂直,
相互垂直,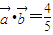 ,且
,且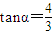 ,求α的值(结果用反三角函数值表示)
,求α的值(结果用反三角函数值表示)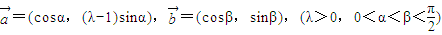 是平面上的两个向量,若向量
是平面上的两个向量,若向量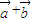 与
与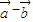 相互垂直,
相互垂直,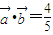 ,且
,且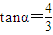 ,求α的值(结果用反三角函数值表示)
,求α的值(结果用反三角函数值表示)