
题目列表(包括答案和解析)
在“探究弹力与弹簧伸长的关系”的实验中。
①关于操作步骤先后顺序,下列说法正确的是
A.先测量原长,后竖直悬挂
B.先竖直悬挂,后测量原长
C.先后顺序对实验结果无影响
D.先后顺序对实验结果的影响程度取决于弹簧的自重
②为了探求弹簧弹力F和弹簧伸长量的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为 .这两根弹簧的劲度系数分别为:甲弹簧为 N/m,乙弹簧为
N/m。若要制作一个精确度较高的弹簧秤,应选弹簧 (填“甲”或“乙”)。
③以下是一位同学准备完成的实验步骤,请你帮这位同学按操作的先后顺序,用字母排列出来是: .
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来.
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式。
F.解释函数表达式中常数的物理意义。
④下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15 | 15 | 15 | 15 | 15 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) |
|
|
|
|
|
请你算出每一次弹簧伸长量,并将结果填在上表的空格内;在图11的坐标上作出F-x图线;并写出曲线的函数表达式(x用cm作单位): ,其中常数的物理意义表示:
在“探究弹力与弹簧伸长的关系”的实验中。
①关于操作步骤先后顺序,下列说法正确的是
A.先测量原长,后竖直悬挂
B.先竖直悬挂,后测量原长
C.先后顺序对实验结果无影响
D.先后顺序对实验结果的影响程度取决于弹簧的自重
②为了探求弹簧弹力F和弹簧伸长量 的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为 .这两根弹簧的劲度系数分别为:甲弹簧为 N/m,乙弹簧为
的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为 .这两根弹簧的劲度系数分别为:甲弹簧为 N/m,乙弹簧为
N/m。若要制作一个精确度较高的弹簧秤,应选弹簧 (填“甲”或“乙”)。
③以下是一位同学准备完成的实验步骤,请你帮这位同学按操作的先后顺序,用字母排列出来是: .
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来.
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式。
F.解释函数表达式中常数的物理意义。
④下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15 | 15 | 15 | 15 | 15 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) | | | | | |


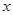 的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为 .这两根弹簧的劲度系数分别为:甲弹簧为 N/m,乙弹簧为
的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为 .这两根弹簧的劲度系数分别为:甲弹簧为 N/m,乙弹簧为| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15 | 15 | 15 | 15 | 15 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) | | | | | |

在“探究弹力与弹簧伸长的关系”的实验中。

①关于操作步骤先后顺序,下列说法正确的是
A.先测量原长,后竖直悬挂
B.先竖直悬挂,后测量原长
C.先后顺序对实验结果无影响
D.先后顺序对实验结果的影响程度取决于弹簧的自重
②为了探求弹簧弹力F和弹簧伸长量 的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为
.这两根弹簧的劲度系数分别为:甲弹簧为
N/m,乙弹簧为
的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为
.这两根弹簧的劲度系数分别为:甲弹簧为
N/m,乙弹簧为
N/m。若要制作一个精确度较高的弹簧秤,应选弹簧 (填“甲”或“乙”)。
③以下是一位同学准备完成的实验步骤,请你帮这位同学按操作的先后顺序,用字母排列出来是: .
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来.
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式。
F.解释函数表达式中常数的物理意义。
④下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
|
弹力(F/N) |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
弹簧原来长度(L0/cm) |
15 |
15 |
15 |
15 |
15 |
|
弹簧后来长度(L/cm) |
16.2 |
17.3 |
18.5 |
19.6 |
20.8 |
|
弹簧伸长量(x/cm) |
|
|
|
|
|
请你算出每一次弹簧伸长量,并将结果填在上表的空格内;在图11的坐标上作出F-x图线;并写出曲线的函数表达式(x用cm作单位): ,其中常数的物理意义表示:

第九部分 稳恒电流
第一讲 基本知识介绍
第八部分《稳恒电流》包括两大块:一是“恒定电流”,二是“物质的导电性”。前者是对于电路的外部计算,后者则是深入微观空间,去解释电流的成因和比较不同种类的物质导电的情形有什么区别。
应该说,第一块的知识和高考考纲对应得比较好,深化的部分是对复杂电路的计算(引入了一些新的处理手段)。第二块虽是全新的内容,但近几年的考试已经很少涉及,以至于很多奥赛培训资料都把它删掉了。鉴于在奥赛考纲中这部分内容还保留着,我们还是想粗略地介绍一下。
一、欧姆定律
1、电阻定律
a、电阻定律 R = ρ![]()
b、金属的电阻率 ρ = ρ0(1 + αt)
2、欧姆定律
a、外电路欧姆定律 U = IR ,顺着电流方向电势降落
b、含源电路欧姆定律

在如图8-1所示的含源电路中,从A点到B点,遵照原则:①遇电阻,顺电流方向电势降落(逆电流方向电势升高)②遇电源,正极到负极电势降落,负极到正极电势升高(与电流方向无关),可以得到以下关系
UA ? IR ? ε ? Ir = UB
这就是含源电路欧姆定律。
c、闭合电路欧姆定律
在图8-1中,若将A、B两点短接,则电流方向只可能向左,含源电路欧姆定律成为
UA + IR ? ε + Ir = UB = UA
即 ε = IR + Ir ,或 I = ![]()
这就是闭合电路欧姆定律。值得注意的的是:①对于复杂电路,“干路电流I”不能做绝对的理解(任何要考察的一条路均可视为干路);②电源的概念也是相对的,它可以是多个电源的串、并联,也可以是电源和电阻组成的系统;③外电阻R可以是多个电阻的串、并联或混联,但不能包含电源。
二、复杂电路的计算
1、戴维南定理:一个由独立源、线性电阻、线性受控源组成的二端网络,可以用一个电压源和电阻串联的二端网络来等效。(事实上,也可等效为“电流源和电阻并联的的二端网络”——这就成了诺顿定理。)
应用方法:其等效电路的电压源的电动势等于网络的开路电压,其串联电阻等于从端钮看进去该网络中所有独立源为零值时的等效电阻。
2、基尔霍夫(克希科夫)定律

a、基尔霍夫第一定律:在任一时刻流入电路中某一分节点的电流强度的总和,等于从该点流出的电流强度的总和。
例如,在图8-2中,针对节点P ,有
I2 + I3 = I1
基尔霍夫第一定律也被称为“节点电流定律”,它是电荷受恒定律在电路中的具体体现。
对于基尔霍夫第一定律的理解,近来已经拓展为:流入电路中某一“包容块”的电流强度的总和,等于从该“包容块”流出的电流强度的总和。
b、基尔霍夫第二定律:在电路中任取一闭合回路,并规定正的绕行方向,其中电动势的代数和,等于各部分电阻(在交流电路中为阻抗)与电流强度乘积的代数和。
例如,在图8-2中,针对闭合回路① ,有
ε3 ? ε2 = I3 ( r3 + R2 + r2 ) ? I2R2
基尔霍夫第二定律事实上是含源部分电路欧姆定律的变体(☆同学们可以列方程 UP = … = UP得到和上面完全相同的式子)。
3、Y?Δ变换

在难以看清串、并联关系的电路中,进行“Y型?Δ型”的相互转换常常是必要的。在图8-3所示的电路中
☆同学们可以证明Δ→ Y的结论…
Rc = ![]()
Rb = ![]()
Ra = ![]()
Y→Δ的变换稍稍复杂一些,但我们仍然可以得到
R1 = ![]()
R2 = ![]()
R3 = ![]()
三、电功和电功率
1、电源
使其他形式的能量转变为电能的装置。如发电机、电池等。发电机是将机械能转变为电能;干电池、蓄电池是将化学能转变为电能;光电池是将光能转变为电能;原子电池是将原子核放射能转变为电能;在电子设备中,有时也把变换电能形式的装置,如整流器等,作为电源看待。
电源电动势定义为电源的开路电压,内阻则定义为没有电动势时电路通过电源所遇到的电阻。据此不难推出相同电源串联、并联,甚至不同电源串联、并联的时的电动势和内阻的值。
例如,电动势、内阻分别为ε1 、r1和ε2 、r2的电源并联,构成的新电源的电动势ε和内阻r分别为(☆师生共同推导…)
ε = ![]()
r = ![]()
2、电功、电功率
电流通过电路时,电场力对电荷作的功叫做电功W。单位时间内电场力所作的功叫做电功率P 。
计算时,只有W = UIt和P = UI是完全没有条件的,对于不含源的纯电阻,电功和焦耳热重合,电功率则和热功率重合,有W = I2Rt = ![]() t和P = I2R =
t和P = I2R =![]() 。
。
对非纯电阻电路,电功和电热的关系依据能量守恒定律求解。
四、物质的导电性
在不同的物质中,电荷定向移动形成电流的规律并不是完全相同的。
1、金属中的电流
即通常所谓的不含源纯电阻中的电流,规律遵从“外电路欧姆定律”。
2、液体导电
能够导电的液体叫电解液(不包括液态金属)。电解液中离解出的正负离子导电是液体导电的特点(如:硫酸铜分子在通常情况下是电中性的,但它在溶液里受水分子的作用就会离解成铜离子Cu2+和硫酸根离子S![]() ,它们在电场力的作用下定向移动形成电流)。
,它们在电场力的作用下定向移动形成电流)。
在电解液中加电场时,在两个电极上(或电极旁)同时产生化学反应的过程叫作“电解”。电解的结果是在两个极板上(或电极旁)生成新的物质。
液体导电遵从法拉第电解定律——
法拉第电解第一定律:电解时在电极上析出或溶解的物质的质量和电流强度、跟通电时间成正比。表达式:m = kIt = KQ (式中Q为析出质量为m的物质所需要的电量;K为电化当量,电化当量的数值随着被析出的物质种类而不同,某种物质的电化当量在数值上等于通过1C电量时析出的该种物质的质量,其单位为kg/C。)
法拉第电解第二定律:物质的电化当量K和它的化学当量成正比。某种物质的化学当量是该物质的摩尔质量M(克原子量)和它的化合价n的比值,即 K = ![]() ,而F为法拉第常数,对任何物质都相同,F = 9.65×104C/mol 。
,而F为法拉第常数,对任何物质都相同,F = 9.65×104C/mol 。
将两个定律联立可得:m = ![]() Q 。
Q 。
3、气体导电
气体导电是很不容易的,它的前提是气体中必须出现可以定向移动的离子或电子。按照“载流子”出现方式的不同,可以把气体放电分为两大类——
a、被激放电
在地面放射性元素的辐照以及紫外线和宇宙射线等的作用下,会有少量气体分子或原子被电离,或在有些灯管内,通电的灯丝也会发射电子,这些“载流子”均会在电场力作用下产生定向移动形成电流。这种情况下的电流一般比较微弱,且遵从欧姆定律。典型的被激放电情形有
b、自激放电
但是,当电场足够强,电子动能足够大,它们和中性气体相碰撞时,可以使中性分子电离,即所谓碰撞电离。同时,在正离子向阴极运动时,由于以很大的速度撞到阴极上,还可能从阴极表面上打出电子来,这种现象称为二次电子发射。碰撞电离和二次电子发射使气体中在很短的时间内出现了大量的电子和正离子,电流亦迅速增大。这种现象被称为自激放电。自激放电不遵从欧姆定律。
常见的自激放电有四大类:辉光放电、弧光放电、火花放电、电晕放电。
4、超导现象
据金属电阻率和温度的关系,电阻率会随着温度的降低和降低。当电阻率降为零时,称为超导现象。电阻率为零时对应的温度称为临界温度。超导现象首先是荷兰物理学家昂尼斯发现的。
超导的应用前景是显而易见且相当广阔的。但由于一般金属的临界温度一般都非常低,故产业化的价值不大,为了解决这个矛盾,科学家们致力于寻找或合成临界温度比较切合实际的材料就成了当今前沿科技的一个热门领域。当前人们的研究主要是集中在合成材料方面,临界温度已经超过100K,当然,这个温度距产业化的期望值还很远。
5、半导体
半导体的电阻率界于导体和绝缘体之间,且ρ
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com