（08年上海卷理）(18分)已知以a₁为首项的数列{a_n}满足：

⑴ 当a₁＝1，c＝1，d＝3时，求数列{a_n}的通项公式

⑵ 当0＜a₁＜1，c＝1，d＝3时，试用a₁表示数列{a_n}的前100项的和S₁₀₀

⑶ 当0＜a₁＜（m是正整数），c＝，d≥3m时，求证：数列a₂－，a_3m+2－，a_6m+2－，a_9m+2－成等比数列当且仅当d＝3m

(本题满分18分，其中第1小题4分，第2小题6分，第,3小题8分)

一青蛙从点开始依次水平向右和竖直向上跳动，其落点坐标依次是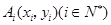，(如图所示，坐标以已知条件为准)，表示青蛙从点到点所经过的路程。

(1) 若点为抛物线准线上

一点，点，均在该抛物线上，并且直线经

过该抛物线的焦点，证明.

(2)若点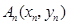要么落在所表示的曲线上，

要么落在所表示的曲线上，并且,

试写出（不需证明）；

(3)若点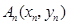要么落在所表示的曲线上，要么落在所表示的曲线上，并且，求的表达式.

（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分其中①6分、②2分。

设抛物线的焦点为，过且垂直于轴的直线与抛物线交于两点，已知.

（1）求抛物线的方程；

（2）设，过点作方向向量为的直线与抛物线相交于两点，求使为钝角时实数的取值范围；

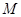
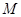（3）①对给定的定点，过作直线与抛物线相交于两点，问是否存在一条垂直于轴的直线与以线段为直径的圆始终相切？若存在，请求出这条直线；若不存在，请说明理由。

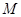②对，过作直线与抛物线相交于两点，问是否存在一条垂直于轴的直线与以线段为直径的圆始终相切？（只要求写出结论，不需用证明）

（本题满分18分，第（1）小题4分，第（2）小题6分，第（3）小题8分）

在平行四边形中，已知过点的直线与线段分别相交于点。若。

（1）求证：与的关系为；

（2）设，定义函数，点列在函数的图像上，且数列是以首项为1，公比为的等比数列，为原点，令，是否存在点，使得？若存在，请求出点坐标；若不存在，请说明理由。

（3）设函数为上偶函数，当时，又函数图象关于直线对称， 当方程在上有两个不同的实数解时，求实数的取值范围。

．．(本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分。

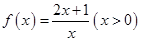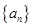设函数，数列满足。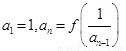

⑴求数列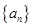的通项公式；

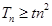⑵设，若对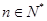恒成立，求实数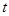的取值范围；

⑶是否存在以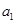为首项，公比为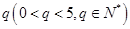的等比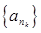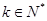数列，，使得数列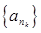中每一项都是数列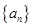中不同的项，若存在，求出所有满足条件的数列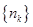的通项公式；若不存在，说明理由。