如图16所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持60°的夹角。若在B点用细绳悬挂一个定滑轮(不计重力)，某人用它匀速地提起重物。已知重物的质量m＝30 kg，人的质量M＝50 kg，连接人的绳子与水平方向的夹角始终保持30°，g取10 m/s²。试求：

(1)此时地面对人的支持力；　　　　　　　　　　　　　　　　　　　

(2)轻杆BC和细绳AB所受的力的大小。(结果可以用根号表示)

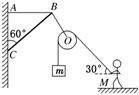图16

图3-1-9

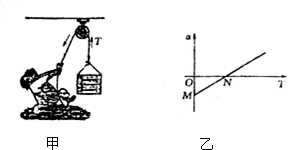如图甲．某人正通过定滑轮将质最为m的货物提升到高处，滑轮的质最和摩擦均不计，货物获得的加速度a与绳子对货物竖直向上的拉力T之问的函数关系如图乙所示．由图可以判断力F作用前相比，物块对斜面的摩挤）J次刹面对地面的摩披力的变化悄祝分别是
①图线与纵轴的交点，M的值a_u=-g．　　
②图线与横轴的交点N的值T_N=mg．
③图线的斜率等于物体的质量m　　　　　　
④图线的斜率等于物体质量的倒数1/m
以上判断正确的是

1. A.
   ④
2. B.
   ②③
3. C.
   ①②③
4. D.
   ①②④

图1-1-17