
题目列表(包括答案和解析)
(本题满分12分)
某高校在2012年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组 ,第二组
,第二组 ,第三组
,第三组 ,第四组
,第四组 ,第五组
,第五组 得到的频率分布直方图如图所示,
得到的频率分布直方图如图所示,

(1)求第三、四、五组的频率;
(2)为了以选拔出最优秀的学生,学校决定在笔试成绩高的第三、四、五组中用分层抽样抽取6名学生进入第二轮面试,求第三、四、五组每组各抽取多少名学生进入第二轮面试。
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的
面试,求第四组至少有一名学生被甲考官面试的概率。
(本题满分12分)
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?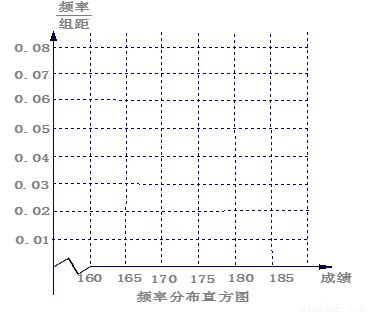
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
5 |
0.050 |
|
第2组 |
|
① |
0.350 |
|
第3组 |
|
30 |
② |
|
第4组 |
|
20 |
0.200 |
|
第5组 |
|
10 |
0.100 |
|
合计 |
100 |
1.000 |
|
(本题满分12分)
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 |  | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 |  | 20 | 0.200 |
| 第5组 |  | 10 | 0.100 |
| 合计 | 100 | 1.000 | |
|
 ,第二组
,第二组 ,第三组
,第三组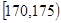 ,第四组
,第四组 ,第五组
,第五组 得到的频率分布直方图如图所示,
得到的频率分布直方图如图所示,
(本题满分12分)甲、乙、丙三个同学同时报名参加某重点高校2010年自主招生,高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即获得自主招生入选资格.因为甲、乙、丙三人各有优势,甲、乙、丙三人审核过关的概率分别为0.5,0.6,0.4,审核过关后,甲、乙、丙三人文化测试合格的概率分别为0.6,0.5,0.75.
(1)求甲、乙、丙三人中只有一人通过审核的概率;
(2)求甲、乙、丙三人各自获得自主招生入选资格的概率;
(3)求甲、乙、丙三人中至少有二人获得自主招生入选资格的概率。
一.选择题
BADCC ACCCC AD
二.填空题
13. 14. 29 15.
14. 29 15. (开闭区间均可) 16. ①
④
(开闭区间均可) 16. ①
④
三、解答题
17.解:
(1)∵ , ∴
, ∴ ,
,
即 ………3分
………3分
则  .
. , ∴
, ∴ ………6分
………6分
(2)由题知 ,得
,得 ,
, ………8分
………8分
得sinB=2cosB, ………10分
………10分
∴



 ………12分
………12分
18.解:
(1)得分为60分,12道题必须全做对。在其余的5道题中,有两道题答对的概率为 ,
,
有一道题答对的概率为 ,还有两道答对的概率为
,还有两道答对的概率为 ………2分
………2分
所以得分为60分的概率为:P= ………4分
………4分
(2)由 可得
可得 ………5分
………5分
得 ,得2<x<15,则x=5或x=10,则相应得分为55分或50分……7分
,得2<x<15,则x=5或x=10,则相应得分为55分或50分……7分
得分为50分表示只做对了10道题,做错2道题,所以概率为

 +
+
+ =
= ………9分
………9分
得分为55分表示只做对了11道题,做错1道题,所以概率为:
P2= =
= ………11分
………11分
则所求概率为 +
+ =
= 。答:该考生得分的概率为
。答:该考生得分的概率为 ………12分
………12分
19.证明:
(1)面A1B
又 面AB
B
(2)由于BC⊥面AB
又 AB
AB ,则AH=
,则AH= 为A到平面VBC的距离………7分
为A到平面VBC的距离………7分
(3)过H作HG⊥VB于G,连AG则∠AGH为二面角A-VB-C的平面角
在Rt B1CB中
B1CB中 ………10分
………10分
又Rt B1HG∽Rt
B1HG∽Rt B1BC 则
B1BC 则 ,即
,即
 故二面角A-VB-C的大小为
故二面角A-VB-C的大小为 ………12分
………12分
(本题也可用建立空间直角坐标系然后用空间向量求解,评分标准参照执行)
20.解:
(1)设{an}的公差d,为{bn}的公比为q,则

 ………6分
………6分
(2){Cn}的前n-1项中共有{an}中的1+2+3+…(n-1)= 个项………8分
个项………8分
且{an}的第 项为
项为 ………10分
………10分
故Cn是首项为 ,公差为2,项数为n的等差数列的前n项和,
,公差为2,项数为n的等差数列的前n项和,
 ………12分
………12分
21.解:
(1)f‘(x)=x2+ax+b,由 f‘(3)=9+
(2)令f‘(x)= x2+ax
当a=-6时,f‘(x)= ≥0,则f(x)无单调递减区间………4分
≥0,则f(x)无单调递减区间………4分
当a>-6时,令f‘(x) =(x-3)(x+a+3)≤0,得-a-3≤x≤3,
则f(x)的单调递减区间为[-a-3,3] ………6分
当a<-6时,易得f(x)的单调递减区间为[3,-a-3]
综上所述当a=-6时, f(x)无单调递减区间;当a>-6时,f(x)的单调递减区间为[-a-3,3],
当a<-6时, f(x)的单调递减区间为[3,-a-3] ………8分
(3)由a>0知-a-3<-3,由(2)知f(x)在[-3,3]上是减函数,又-3≤3cos ≤3,-3≤3sin
≤3,-3≤3sin ≤3,则要
≤3,则要 恒成立只要|f(-3)-f(3)|<72恒成立………10分
恒成立只要|f(-3)-f(3)|<72恒成立………10分
又|f(-3)-f(3)|=18|a+2|<72,得-6<a<2,又a>0,则0<a<2………12分
22.解:
(1)由题意设椭圆方程为 ………1分
………1分
则 ,椭圆方程为
,椭圆方程为 ………4分
………4分
(2)设 ,
,
则 ………7分
………7分
又 则
则
 ………9分
………9分
则 =
=
 ………11分
………11分
由于 ,
,

因此 的取值范围为
的取值范围为 ………14分
………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com