
题目列表(包括答案和解析)
设点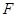 是抛物线
是抛物线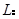
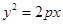
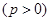 的焦点,
的焦点,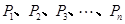 是抛物线
是抛物线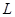 上的
上的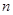 个不同的点(
个不同的点(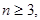
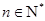 ).
).
(1) 当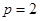 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、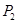 、
、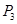 的坐标,从而使得
的坐标,从而使得
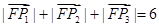 ;
;
(2)当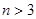 时,若
时,若 ,
,
求证: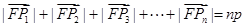 ;
;
(3) 当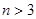 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若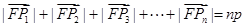 ,则
,则 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数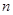 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
【解析】第一问利用抛物线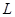 的焦点为
的焦点为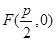 ,设
,设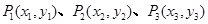 ,
,
分别过 作抛物线
作抛物线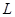 的准线
的准线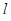 的垂线,垂足分别为
的垂线,垂足分别为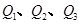 .
.
由抛物线定义得到
第二问设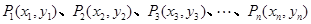 ,分别过
,分别过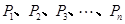 作抛物线
作抛物线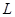 的准线
的准线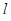 垂线,垂足分别为
垂线,垂足分别为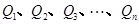 .
.
由抛物线定义得
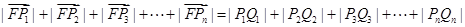

第三问中①取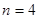 时,抛物线
时,抛物线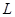 的焦点为
的焦点为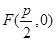 ,
,
设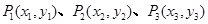 ,
, 分别过
分别过
 作抛物线
作抛物线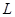 的准线
的准线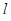 垂线,垂足分别为
垂线,垂足分别为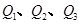
 .由抛物线定义得
.由抛物线定义得
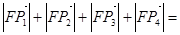
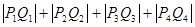
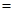
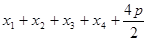
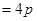 ,
,
则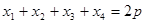 ,不妨取
,不妨取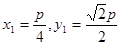 ;
;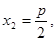
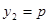 ;
;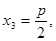
 ;
;
解:(1)抛物线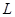 的焦点为
的焦点为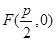 ,设
,设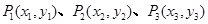 ,
,
分别过 作抛物线
作抛物线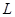 的准线
的准线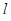 的垂线,垂足分别为
的垂线,垂足分别为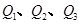 .由抛物线定义得
.由抛物线定义得
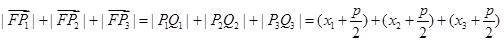
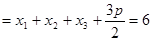
因为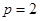 ,所以
,所以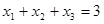 ,
,
故可取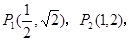
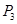
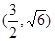 满足条件.
满足条件.
(2)设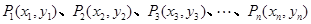 ,分别过
,分别过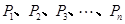 作抛物线
作抛物线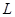 的准线
的准线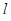 垂线,垂足分别为
垂线,垂足分别为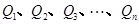 .
.
由抛物线定义得
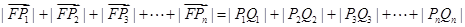
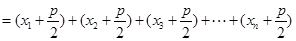
 又因为
又因为
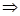
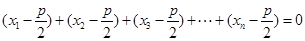
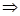
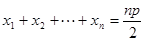 ;
;
所以

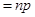 .
.
(3) ①取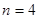 时,抛物线
时,抛物线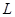 的焦点为
的焦点为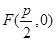 ,
,
设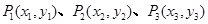 ,
, 分别过
分别过
 作抛物线
作抛物线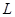 的准线
的准线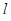 垂线,垂足分别为
垂线,垂足分别为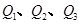
 .由抛物线定义得
.由抛物线定义得
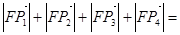
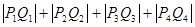
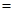
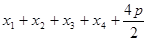
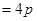 ,
,
则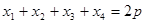 ,不妨取
,不妨取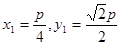 ;
;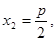
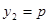 ;
;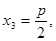
 ;
; ,
,
则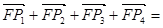
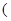
 ,
,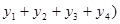
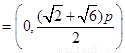
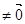 .
.
故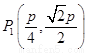 ,
,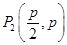 ,
,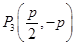 ,
,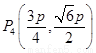 是一个当
是一个当 时,该逆命题的一个反例.(反例不唯一)
时,该逆命题的一个反例.(反例不唯一)
② 设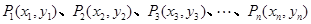 ,分别过
,分别过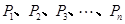 作
作
抛物线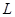 的准线
的准线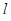 的垂线,垂足分别为
的垂线,垂足分别为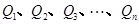 ,
,
由 及抛物线的定义得
及抛物线的定义得
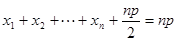 ,即
,即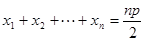 .
.
因为上述表达式与点 的纵坐标无关,所以只要将这
的纵坐标无关,所以只要将这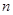 点都取在
点都取在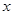 轴的上方,则它们的纵坐标都大于零,则
轴的上方,则它们的纵坐标都大于零,则

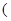
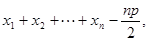
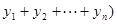

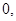
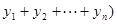 ,
,
而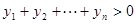 ,所以
,所以 .
.
(说明:本质上只需构造满足条件且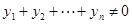 的一组
的一组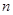 个不同的点,均为反例.)
个不同的点,均为反例.)
③ 补充条件1:“点 的纵坐标
的纵坐标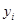 (
(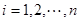 )满足
)满足 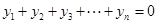 ”,即:
”,即:
“当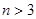 时,若
时,若 ,且点
,且点 的纵坐标
的纵坐标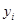 (
(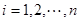 )满足
)满足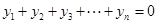 ,则
,则 ”.此命题为真.事实上,设
”.此命题为真.事实上,设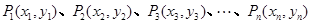 ,
,
分别过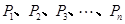 作抛物线
作抛物线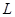 准线
准线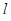 的垂线,垂足分别为
的垂线,垂足分别为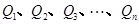 ,由
,由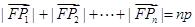 ,
,
及抛物线的定义得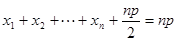 ,即
,即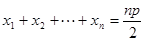 ,则
,则

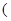
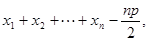
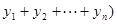

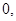
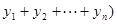 ,
,
又由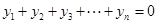 ,所以
,所以 ,故命题为真.
,故命题为真.
补充条件2:“点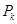 与点
与点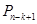
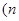 为偶数,
为偶数,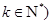 关于
关于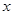 轴对称”,即:
轴对称”,即:
“当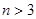 时,若
时,若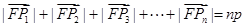 ,且点
,且点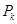 与点
与点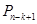
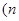 为偶数,
为偶数,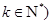 关于
关于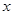 轴对称,则
轴对称,则 ”.此命题为真.(证略)
”.此命题为真.(证略)
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,若对任意
,若对任意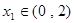 ,
,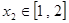 ,不等式
,不等式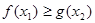 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【解析】第一问利用 的定义域是
的定义域是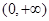
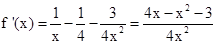
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数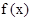 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意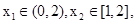 不等式
不等式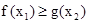 恒成立,问题等价于
恒成立,问题等价于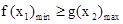 只需研究最值即可。
只需研究最值即可。
解: (I) 的定义域是
的定义域是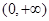 ......1分
......1分
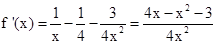 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数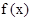 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分
(II)若对任意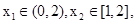 不等式
不等式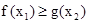 恒成立,
恒成立,
问题等价于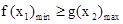 ,
.........5分
,
.........5分
由(I)可知,在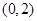 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,所以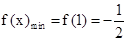 ; ............6分
; ............6分
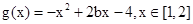
当b<1时,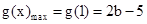 ;
;
当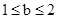 时,
时, ;
;
当b>2时,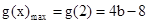 ;
............8分
;
............8分
问题等价于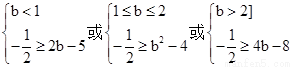
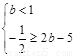 ........11分
........11分
解得b<1 或 或
或  即
即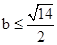 ,所以实数b的取值范围是
,所以实数b的取值范围是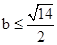
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为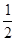 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q;
【解析】(1)离心率为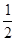 得
得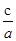 =
=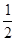 ,椭圆的短半轴为半径的圆与直线x-y+
,椭圆的短半轴为半径的圆与直线x-y+ =0相切,b=
=0相切,b= =
=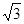 ,解得a2=4,b2=3;(Ⅱ)直线PB的方程为y=k(x-4)
,解得a2=4,b2=3;(Ⅱ)直线PB的方程为y=k(x-4)
已知函数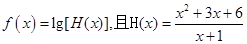 ,
,
(1)求函数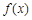 的定义域;
的定义域;
(2)求函数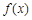 在区间
在区间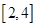 上的最小值;
上的最小值;
(3)已知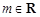 ,命题p:关于x的不等式
,命题p:关于x的不等式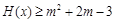 对函数
对函数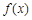 的定义域上的任意
的定义域上的任意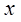 恒成立;命题q:指数函数
恒成立;命题q:指数函数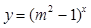 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
【解析】第一问中,利用由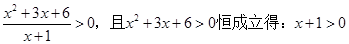 即
即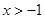
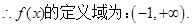
第二问中,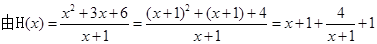 ,
,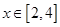 得:
得:
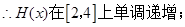
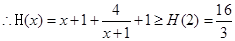 ,
,
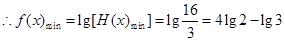
第三问中,由在函数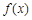 的定义域上
的任意
的定义域上
的任意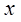 ,
,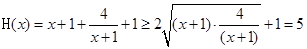 ,当且仅当
,当且仅当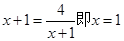 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,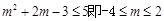 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时;当命题p为假,命题q为真时分为两种情况讨论即可 。
解:(1)由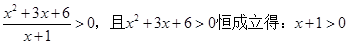 即
即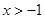
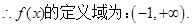
(2)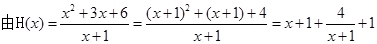 ,
,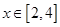 得:
得:
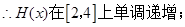
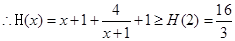 ,
,
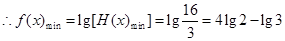
(3)由在函数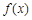 的定义域上
的任意
的定义域上
的任意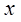 ,
,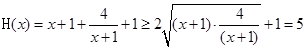 ,当且仅当
,当且仅当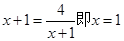 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,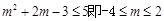 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时,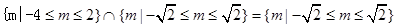
当命题p为假,命题q为真时,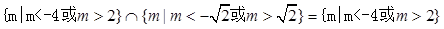 ,
,
所以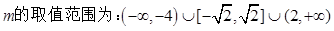
乒乓球比赛规则规定,一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分。设在甲、乙的比赛中,每次发球,发球1分的概率为0.6,各次发球的胜负结果相互独立。甲、乙的一局比赛中,甲先发球。
(I) 求开球第4次发球时,甲、乙的比分为1比2的概率;
(II) 求开始第5次发球时,甲得分领先的概率。
【解析】本试题主要是考查了关于独立事件的概率的求解,以及分布列和期望值问题。首先要理解发球的具体情况,然后对于事件的情况分析,讨论,并结合独立事件的概率求解结论。
【点评】首先从试题的选材上来源于生活,同学们比较熟悉的背景,同时建立在该基础上求解进行分类讨论的思想的运用,以及能结合独立事件的概率公式求解分布列的问题。情景比较亲切,容易入手,但是在讨论情况的时候,容易丢情况。
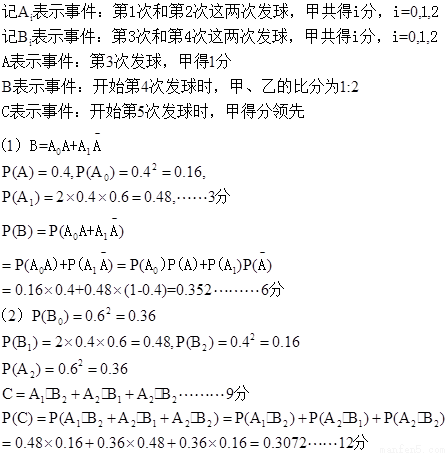
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com