
题目列表(包括答案和解析)
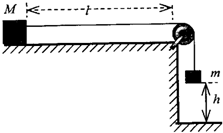 如图所示,水平平台的右端安装有滑轮,质量为M的物块放在与滑轮相距l的平台上,物块与平台间的动摩擦因数为μ现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m的小球,绳拉直时用手托住小球使其在距地面h高处静止,重力加速度为g.设最大静摩擦力等于滑动摩擦力(g取10m/s2).
如图所示,水平平台的右端安装有滑轮,质量为M的物块放在与滑轮相距l的平台上,物块与平台间的动摩擦因数为μ现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m的小球,绳拉直时用手托住小球使其在距地面h高处静止,重力加速度为g.设最大静摩擦力等于滑动摩擦力(g取10m/s2). 如图所示,水平平台的右端安装有定滑轮(大小忽略不计),质量M=2kg的物块A放在平台上与滑轮相距L=2.5m,物块A与平台的动摩擦因数μ=0.2.现有一轻绳跨过定滑轮,左端与物块A相连,另一端挂质量为m的物体B,绳拉直时用手托住物体B停在距离地面h=0.5m处静止不动.某时刻放开物体B,着地后物体B立即停止运动,要使物块A不撞到定滑轮,物体B的质量m应满足什么条件?(g取10m/s2)
如图所示,水平平台的右端安装有定滑轮(大小忽略不计),质量M=2kg的物块A放在平台上与滑轮相距L=2.5m,物块A与平台的动摩擦因数μ=0.2.现有一轻绳跨过定滑轮,左端与物块A相连,另一端挂质量为m的物体B,绳拉直时用手托住物体B停在距离地面h=0.5m处静止不动.某时刻放开物体B,着地后物体B立即停止运动,要使物块A不撞到定滑轮,物体B的质量m应满足什么条件?(g取10m/s2)如图所示,水平平台的右端安装有滑轮,质量为M的物块放在与滑轮相距l 的平台上,物块与平台间的动摩擦因数为μ。现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m的小球,绳拉直时用手托住小球使其在距地面h高处静止,重力加速度为g.设最大静摩擦力等于滑动摩擦力(g取10 m/s2).
1. 放开小球,系统运动,求小球做匀加速运动时的加速度及此时绳子的拉力大小.
2.设M=2kg,,l=2.5 m,h=0. 5 m,μ=0.2,小球着地后立即停止运动,要使物块不撞到定滑轮,则小球质量m应满足什么条件?
如图所示,水平平台的右端安装有定滑轮,质量M的物块放在平台上与滑轮相距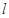 处,M与平台的动摩擦因数
处,M与平台的动摩擦因数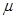 ,现有一轻绳跨过定滑轮,右端与M连,另一端挂质量
,现有一轻绳跨过定滑轮,右端与M连,另一端挂质量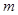 物块,绳拉直时用手托住
物块,绳拉直时用手托住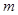 停在距地面h高度处静止。(不计定滑轮的质量和摩擦)。
停在距地面h高度处静止。(不计定滑轮的质量和摩擦)。
(1)放开m,求出M运动时加速度及此时绳子的拉力大小。
(2)设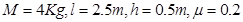 ,
,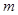 物块着地后立即停止运动,要M物块能运动起来而不撞到定滑轮,质量m应满足什么条件?
物块着地后立即停止运动,要M物块能运动起来而不撞到定滑轮,质量m应满足什么条件? 
如图所示,水平平台的右端安装有滑轮,质量为M=2.0kg的物块放在与滑轮相距L=2.5m的平台上,物块与平台间的动摩擦因数为μ=0.2.现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m的小球,绳拉直时用手托住小球使其在距地面h高处静止,设最大静摩擦力等于滑动摩擦力,取g="10" m/s2,要求:
(1)取m=1.0kg,放开小球,系统运动,求小球做匀加速运动时的加速度大小a以及此时绳子的拉力大小T;
(2)取m=1.0kg,放开小球,系统运动,小球着地后立即停止运动,要使物块M刚好能运动到右端滑轮处,则小球静止时距地面的高度h至少为多大;
(3)取h="0.5" m,小球着地后立即停止运动,要使物块撞不到定滑轮,求小球质量m的取值范围.
一单项选择题:本题共6小题,每小题3分,共18分
1. 1.D 2.A 3.C 4.B 5.D 6.A
二多项选择题:本题共5小题,每小题4分,共20分。全部选对的得4分,选对但不全的得2分,错选或不答的得0分
7.ABD 8.BC 9.ABC 10.AD 11.ACD
三实验题:本题共 2小题,共 23分
12.(1)1.880(1.881给分) (2分); 1.044 (2分)
(2)①
13.
 (1) 图 (3分) (2) 0-3V(2分) R1 (2分) (3) 图(4分)
(1) 图 (3分) (2) 0-3V(2分) R1 (2分) (3) 图(4分)

四 计算或论述题
14.地球绕太阳运动  3分
3分
太阳的质量
 3分
3分
(2)设小行星运行周期为T1  2分
2分
对小行星: 2分
2分
∴R1= 2分
2分
∴小行星与地球最近距离S=R1?R= 2分
2分
15.解:(1)由粒子的飞行轨迹,利用左手定则可知,该粒子带负电荷.粒子由A点射入,由C点飞出,其速度方向改变了90°,则粒子轨迹半径
 2分
2分
又  2分
2分
则粒子的比荷  2分
2分
(2)粒子从D点飞出磁场速度方向改变了60°角,故AD弧所对圆心角60°,粒子做圆周运动的半径

 2分
2分
又  2分
2分
所以  2分
2分
粒子在磁场中飞行时间
 2分
2分
16. (1)设共同加速度a,绳拉力F
有 mg-F=ma
F-μMg=Ma 3分
得到
 4分
4分
(2)当M运动h距离时速度为v,  1分
1分
又M运动s距离停止,由动能定理
 2分
2分
M物块不撞到定滑轮满足  1分
1分
得到 
代入得  2分
2分
因为要拉动M  结果是
结果是  2分
2分
17.(1) 要求当R=0时, E/R0≤I0
所以 R0≥E/ I0 3分
(2) 电量-q的粒子经过电压U加速后速度v0

 2分
2分
粒子进入Q场区域做半径r0,的匀速圆周运动
 2分
2分


 3分
3分
显然加速电压U 与与-q没有关系,所以只要满足上面关系,不同的负电荷都能绕Q做半径r0,的匀速圆周运动。
(3) 
即
 3分
3分
 2分
2分
18.(1)最大速度时拉力与安培力合力为零
P/v0-BIL=0 E=BL v。 I=E/(R+ R0)
即  3分
3分
 2分
2分
(2)由能量关系,产生总电热Q

 2分
2分
R电阻上所产生的电热
 2分
2分
(3) 
由(1)问可知 F=2P/v0 2分
当速度为v0时加速度a  2分
2分
解得

 2分
2分
19.(1)AB第一次与挡板碰后 A返回速度为v0
由动量守恒定律得 mA v0=(mA+mB) v1
∴v1=
(2)A相对于B滑行ΔS1
由动能定理得
μmAgΔS1= v02-
v02- (mA+mB) v12
(mA+mB) v12
ΔS1==
(3)AB与N碰撞后,返回速度大小为v2,则v2= v1
B与M相碰后停止,设A减速至零A相对B滑行ΔS1/
-μmAgΔS1/=0- v22 ΔS1/=
v22 ΔS1/=
∴A能与M碰撞第二次 3分
(4) A与M第一次碰撞速度为v1(v1= v0)
mA v1(mA+mB) v1/ ∴ v1/= v1
v1
A相对于B滑行ΔS1
μmAgΔS1= v12
v12 (mA+mB) v1/2
(mA+mB) v1/2
ΔS1= 2分
2分
当B再次与M相碰而静止时,A相对于B能滑行的最大距离为Sm1
0-v1/2=-2μg Sm1
Sm1= >ΔS1
>ΔS1
同理 每次以共同速度相碰,A都能相对B滑行到与M相碰,最终都停在M处 1分
A与M第二次碰撞速度为v2
则v22-v1/2=-2μgΔS1
v22= v12-2μgΔS1=
v12-2μgΔS1= ×6ΔS1-2ΔS1=
×6ΔS1-2ΔS1= ΔS1
ΔS1
同理ΔS2= =
= ΔS1
2分
ΔS1
2分
依次类推ΔS3== ΔS2
ΔS2
ΔS=(ΔS1+ΔS2+ΔS3+……) 2=
2= 2分
2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com