
题目列表(包括答案和解析)
 一个进口时,只有乘积是3的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.
一个进口时,只有乘积是3的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.
 一个进口时,只有乘积是3的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.
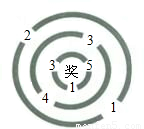
一个进口时,只有乘积是3的倍数,才可以进入迷宫中心,现让小军从最外环任一个进口进入.如图,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.
(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.
(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规定:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?![]() 如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.
如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.

一.选择题
1. D 2.A 3.C 4.B 5.A 6.D 7.A 8.A 9.B 10.A
二.填空题
11. 4(m+%20.files/image240.gif) +1)(m-
+1)(m-%20.files/image240.gif) +1) 12.
-8 13.
+1) 12.
-8 13.
14. %20.files/image243.gif) 15. 553 16. 10
15. 553 16. 10
三.解答题
17.解:%20.files/image245.gif) ,
, %20.files/image247.gif) (2分)
(2分)
%20.files/image249.gif) (4分)
(4分)
%20.files/image251.gif) (5分)
(5分)
18.解:(1)特征1:都是轴对称图形;特征2:都是中心对称图形;特征3:这些图形的面积都等于4个单位面积;等
(2)满足条件的图形有很多,只要画正确一个,都可以得满分.
%20.files/image252.gif) |
19.解:(1)矩形%20.files/image254.gif) ,矩形
,矩形%20.files/image256.gif) ;
;
或菱形%20.files/image258.gif) ;
;
或直角梯形%20.files/image260.gif) ,
,%20.files/image262.gif) 等.
等.
(2)选择%20.files/image254.gif) 是矩形.
是矩形.
证明:∵ABCDEF是正六边形,
%20.files/image265.gif) ,
,%20.files/image267.gif) ,
,%20.files/image269.gif) .
.
同理可证%20.files/image271.gif) .
.
%20.files/image273.gif) 四边形
四边形%20.files/image254.gif) 是矩形.
是矩形.
选择四边形%20.files/image258.gif) 是菱形.
是菱形.
证明:同理可证:%20.files/image277.gif) ,
,%20.files/image279.gif) ,
,
%20.files/image281.gif) ,
,%20.files/image283.gif) .
.
%20.files/image273.gif) 四边形
四边形%20.files/image258.gif) 是平行四边形.
是平行四边形.
又∵BC=DE,%20.files/image287.gif) ,
,%20.files/image289.gif) ,
,
%20.files/image291.gif) .
.
%20.files/image293.gif) .
.
%20.files/image273.gif) 四边形
四边形%20.files/image258.gif) 是菱形.
是菱形.
选择四边形%20.files/image297.gif) 是直角梯形.
是直角梯形.
证明:同理可证:%20.files/image299.gif) ,
,%20.files/image301.gif) ,又由
,又由%20.files/image201.gif) 与
与%20.files/image304.gif) 不平行,
不平行,
得四边形%20.files/image297.gif) 是直角梯形.
是直角梯形.
20.解:(1)%20.files/image306.gif) 甲=
甲=%20.files/image307.gif) (万元);
(万元);
%20.files/image306.gif) 乙=
乙=%20.files/image308.gif) (万元); ……………………(2分)
(万元); ……………………(2分)
甲、乙两商场本周获利都是21万元; ……………………………………(4分)
(2)甲、乙两商场本周每天获利的折线图如图2所示:
%20.files/image309.gif)
…………………………………(6分)
(3)从折线图上看到:乙商场后两天的销售情况都好于甲商场,所以,下周一乙商场获利会多一些. ……………………………(8分)
21.解:(1)%20.files/image311.gif)
%20.files/image313.gif) ??????????????????????????????????????????????????????????????????????????????????? 2分
??????????????????????????????????????????????????????????????????????????????????? 2分
(2)由题意得:
%20.files/image315.gif)
%20.files/image317.gif)
%20.files/image319.gif)
即购%20.files/image117.gif) 种树不少于400棵????????????????????????????????????????????????????????????????????????????????? 5分
种树不少于400棵????????????????????????????????????????????????????????????????????????????????? 5分
(3)%20.files/image322.gif)
%20.files/image324.gif)
%20.files/image326.gif)
%20.files/image328.gif) ?????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
?????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
%20.files/image330.gif) 随
随%20.files/image122.gif) 的增大而减小
的增大而减小
%20.files/image273.gif) 当
当%20.files/image334.gif) 时,购树费用最低为
时,购树费用最低为%20.files/image336.gif) (元)
(元)
当%20.files/image334.gif) 时,
时,%20.files/image339.gif)
%20.files/image273.gif) 此时应购
此时应购%20.files/image117.gif) 种树600棵,
种树600棵,%20.files/image119.gif) 种树300棵???????????????????????????????????????????????????????? 8分
种树300棵???????????????????????????????????????????????????????? 8分
22.(1)树状图略.%20.files/image344.gif) .(2)不公平,理由如下:法一:由树状图可知,
.(2)不公平,理由如下:法一:由树状图可知,%20.files/image346.gif) ,
,%20.files/image348.gif) ,
,%20.files/image350.gif) .
.
所以不公平.法二:从(1)中树状图得知,不是5的倍数时,结果是奇数的有2种情况,而结果是偶数的有6种情况,显然小李胜面大,所以不公平.法三:由于积是5的倍数时两人得分相同,所以可直接比较积不是5的倍数时,奇数、偶数的概率. P(奇数)=%20.files/image352.gif) ,P(偶数)=
,P(偶数)=%20.files/image354.gif) ,所以不公平.可将第二道环上的数4改为任一奇数.(3)设小军x次进入迷宫中心,则2x+3(10-x)≤28,解之得x≥2.所以小军至少2次进入迷宫中心.
,所以不公平.可将第二道环上的数4改为任一奇数.(3)设小军x次进入迷宫中心,则2x+3(10-x)≤28,解之得x≥2.所以小军至少2次进入迷宫中心.
23.解:(1)∵%20.files/image358.gif) ,
,%20.files/image360.gif) ,
,
∴%20.files/image362.gif) 是等边三角形.
是等边三角形.
∴%20.files/image364.gif) .
.
(2)∵CP与%20.files/image152.gif) 相切,
相切,
∴%20.files/image366.gif) .
.
又∵%20.files/image372.gif) (4,0),∴
(4,0),∴%20.files/image374.gif) .∴
.∴%20.files/image376.gif) .
.
∴%20.files/image378.gif) .
.
(3)①过点%20.files/image380.gif) 作
作%20.files/image382.gif) ,垂足为
,垂足为%20.files/image384.gif) ,延长
,延长%20.files/image386.gif) 交
交%20.files/image388.gif) 于
于%20.files/image390.gif) ,
,
∵%20.files/image392.gif) 是半径, ∴
是半径, ∴%20.files/image394.gif) ,∴
,∴%20.files/image396.gif) ,
,
∴%20.files/image398.gif) 是等腰三角形.
是等腰三角形.
又∵%20.files/image362.gif) 是等边三角形,∴
是等边三角形,∴%20.files/image401.gif) =2 .
=2 .
②解法一:过%20.files/image372.gif) 作
作%20.files/image404.gif) ,垂足为
,垂足为%20.files/image406.gif) ,延长
,延长%20.files/image408.gif) 交
交%20.files/image388.gif) 于
于%20.files/image411.gif) ,
,%20.files/image413.gif) 与
与%20.files/image415.gif) 轴交于
轴交于%20.files/image417.gif) ,
,
∵%20.files/image372.gif) 是圆心, ∴
是圆心, ∴%20.files/image420.gif) 是
是%20.files/image422.gif) 的垂直平分线. ∴
的垂直平分线. ∴%20.files/image424.gif) .
.
∴%20.files/image426.gif) 是等腰三角形,
是等腰三角形,
过点%20.files/image411.gif) 作
作%20.files/image429.gif) 轴于
轴于%20.files/image431.gif) ,
,
在%20.files/image433.gif) 中,∵
中,∵%20.files/image435.gif) ,
,
∴%20.files/image437.gif) .∴点
.∴点%20.files/image411.gif) 的坐标(4+
的坐标(4+%20.files/image440.gif) ,
,%20.files/image442.gif) ).
).
在%20.files/image444.gif) 中,∵
中,∵%20.files/image446.gif) ,
,
∴%20.files/image448.gif) .∴
.∴%20.files/image380.gif) 点坐标(2,
点坐标(2,%20.files/image451.gif) ).
).
设直线%20.files/image453.gif) 的关系式为:
的关系式为:%20.files/image455.gif) ,则有
,则有
%20.files/image457.gif) 解得:
解得:%20.files/image459.gif)
∴%20.files/image461.gif) .
.
当%20.files/image463.gif) 时,
时,%20.files/image465.gif) .
.
∴%20.files/image467.gif) .
.
解法二: 过A作%20.files/image404.gif) ,垂足为
,垂足为%20.files/image406.gif) ,延长
,延长%20.files/image408.gif) 交
交%20.files/image388.gif) 于
于%20.files/image411.gif) ,
,%20.files/image413.gif) 与
与%20.files/image415.gif) 轴交于
轴交于%20.files/image417.gif) ,
,
∵%20.files/image372.gif) 是圆心, ∴
是圆心, ∴%20.files/image420.gif) 是
是%20.files/image422.gif) 的垂直平分线. ∴
的垂直平分线. ∴%20.files/image424.gif) .
.
∴%20.files/image426.gif) 是等腰三角形.
是等腰三角形.
∵%20.files/image364.gif) ,∴
,∴%20.files/image478.gif) .
.
∵%20.files/image420.gif) 平分
平分%20.files/image481.gif) ,∴
,∴%20.files/image483.gif) .
.
∵%20.files/image362.gif) 是等边三角形,
是等边三角形,%20.files/image486.gif) , ∴
, ∴%20.files/image488.gif) .
.
∴%20.files/image490.gif) .
.
∴%20.files/image492.gif) 是等腰直角三角形.
是等腰直角三角形.
∴%20.files/image494.gif) .
.
∴%20.files/image496.gif) .
.
24.(1)解:%20.files/image498.gif)
%20.files/image499.gif)
%20.files/image499.gif)
%20.files/image273.gif)
%20.files/image502.gif) (2分) 解得
(2分) 解得 %20.files/image504.gif)
%20.files/image506.gif) (2分)
(2分)
(2)%20.files/image508.gif)
%20.files/image510.gif)
%20.files/image512.gif) (3分)
(3分)
%20.files/image514.gif)
%20.files/image516.gif)
%20.files/image518.gif)
%20.files/image520.gif)
%20.files/image522.gif) (5分)
(5分)
当%20.files/image524.gif)
%20.files/image526.gif)
%20.files/image528.gif)
%20.files/image530.gif)
%20.files/image532.gif) (7分)
(7分)
当%20.files/image534.gif)
%20.files/image536.gif)
%20.files/image538.gif)
%20.files/image540.gif)
%20.files/image542.gif) (9分)
(9分)
%20.files/image544.gif) (10分)
(10分)
25.解:如图,
(1)点%20.files/image210.gif) 移动的过程中,
移动的过程中,%20.files/image212.gif) 能成为
能成为%20.files/image548.gif) 的等腰三角形.
的等腰三角形.
此时点%20.files/image210.gif) 的位置分别是:
的位置分别是:
①%20.files/image203.gif) 是
是%20.files/image205.gif) 的中点,
的中点,%20.files/image207.gif) 与
与%20.files/image117.gif) 重合.
重合.
②%20.files/image555.gif) .③
.③%20.files/image203.gif) 与
与%20.files/image117.gif) 重合,
重合,%20.files/image207.gif) 是
是%20.files/image045.gif) 的中点.(4分)
的中点.(4分)
(2)在%20.files/image561.gif) 和
和%20.files/image563.gif) 中,
中,
%20.files/image565.gif) ,
,%20.files/image567.gif) ,
,
%20.files/image569.gif) .
.
又%20.files/image571.gif) ,
,
%20.files/image573.gif) .
.
%20.files/image575.gif) .
.
%20.files/image582.gif) .(8分)
.(8分)
(3)%20.files/image228.gif) 与
与%20.files/image230.gif) 相切.
相切.
%20.files/image586.gif) ,
,
%20.files/image588.gif) .
.
%20.files/image590.gif) .
.
即%20.files/image592.gif) .
.
又%20.files/image594.gif) ,
,
%20.files/image596.gif) .
.
%20.files/image598.gif) .
.
%20.files/image600.gif) 点
点%20.files/image137.gif) 到
到%20.files/image041.gif) 和
和%20.files/image228.gif) 的距离相等.
的距离相等.
%20.files/image605.gif) 与
与%20.files/image230.gif) 相切,
相切,
%20.files/image600.gif) 点
点%20.files/image137.gif) 到
到%20.files/image228.gif) 的距离等于
的距离等于%20.files/image230.gif) 的半径.
的半径.
%20.files/image608.gif) 与
与%20.files/image230.gif) 相切.(12分)
相切.(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com