（本小题满分13分）

某产品按行业生产标准分成8个等级，等级系数X依次为1,2，……，8，其中X≥5为标准A，X≥3为标准B，已知甲厂执行标准A生产该产品，产品的零售价为6元/件；乙厂执行标准B生产该产品，产品的零售价为4元/件，假定甲、乙两厂得产品都符合相应的执行标准

（I）已知甲厂产品的等级系数X₁的概率分布列如下所示：

且X₁的数字期望EX₁=6，求a，b的值；

（II）为分析乙厂产品的等级系数X₂，从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下：

             3   5   3   3   8   5   5   6   3   4

             6   3   4   7   5   3   4   8   5   3

8   3   4   3   4   4   7   5   6   7

用这个样本的频率分布估计总体分布，将频率视为概率，求等级系数X₂的数学期望.

     在（I）、（II）的条件下，若以“性价比”为判断标准，则哪个工厂的产品更具可购买性？说明理由.

注：（1）产品的“性价比”=；

   （2）“性价比”大的产品更具可购买性.

（本小题满分12分）甲乙两个学校高三年级分别有1200人，1000人，为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：

    甲校：

    乙校：

（Ⅰ）计算x，y的值。

（Ⅱ）若规定考试成绩在[120,150]内为优秀，请分别估计两个学校数学成绩的优秀率。

（Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异。

参考数据与公式：

由列联表中数据计算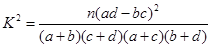

临界值表

（本小题满分14分）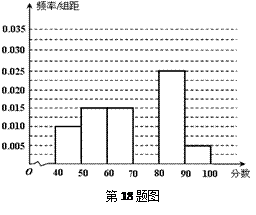


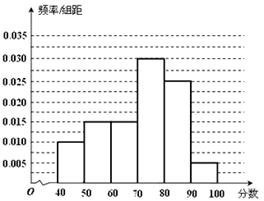
某校从参加高一年级期中考试的学生中随机抽取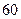名学生，将其数学成绩（均为整数）分成六段
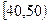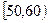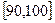，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：
(1)求分数在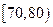内的频率，并补全这个频率分布直方图；
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
（3）用分层抽样的方法在分数段为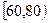的学生中抽取一个容量为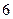的样本，将该样本看成一个总体，从中任取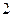人，求至多有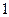人在分数段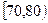的概率.

（本小题满分13分）

某产品按行业生产标准分成8个等级，等级系数X依次为1,2，……，8，其中X≥5为标准A，X≥为标准B，已知甲厂执行标准A生产该产品，产品的零售价为6元/件；乙厂执行标准B生产该产品，产品的零售价为4元/件，假定甲、乙两厂得产品都符合相应的执行标准

（I）已知甲厂产品的等级系数X₁的概率分布列如下所示：

且X₁的数字期望EX₁=6，求a，b的值；

（II）为分析乙厂产品的等级系数X₂，从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下：

             3   5   3   3   8   5   5   6   3   4

             6   3   4   7   5   3   4   8   5   3

8   3   4   3   4   4   7   5   6   7

用这个样本的频率分布估计总体分布，将频率视为概率，求等级系数X₂的数学期望．

   （III）在（I）、（II）的条件下，若以“性价比”为判断标准，则哪个工厂的产品更具可购买性？说明理由．

注：（1）产品的“性价比”=；

      （2）“性价比”大的产品更具可购买性．

（本小题满分13分）
某产品按行业生产标准分成8个等级，等级系数X依次为1,2，……，8，其中X≥5为标准A，X≥3为标准B，已知甲厂执行标准A生产该产品，产品的零售价为6元/件；乙厂执行标准B生产该产品，产品的零售价为4元/件，假定甲、乙两厂得产品都符合相应的执行标准
（I）已知甲厂产品的等级系数X₁的概率分布列如下所示：

且X₁的数字期望EX₁=6，求a，b的值；
（II）为分析乙厂产品的等级系数X₂，从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下：
3   5   3   3   8   5   5   6   3   4
6   3   4   7   5   3   4   8   5   3
8   3   4   3   4   4   7   5   6   7
用这个样本的频率分布估计总体分布，将频率视为概率，求等级系数X₂的数学期望.
        在（I）、（II）的条件下，若以“性价比”为判断标准，则哪个工厂的产品更具可购买性？说明理由.
注：（1）产品的“性价比”=；
（2）“性价比”大的产品更具可购买性.