
题目列表(包括答案和解析)
(本题满分15分)已知 在定义域上是奇函数,且在
在定义域上是奇函数,且在 上是减函数,图像如图所示.
上是减函数,图像如图所示.
(1)化简: ;
;
(2)画出函数 在
在 上的图像;
上的图像;
(3)证明: 在
在 上是减函数.
上是减函数.

(本题满分15分)
如图:某污水处理厂要在一个矩形污水处理池 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道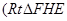 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
.
(Ⅰ)试将污水净化管道的长度 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
(Ⅱ)问:当 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.

(本题满分15分)已知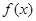 在定义域上是奇函数,且在
在定义域上是奇函数,且在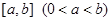 上是减函数,图像如图所示.
上是减函数,图像如图所示.
(1)化简: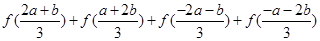 ;
;
(2)画出函数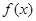 在
在 上的图像;
上的图像;
(3)证明: 在
在 上是减函数.
上是减函数.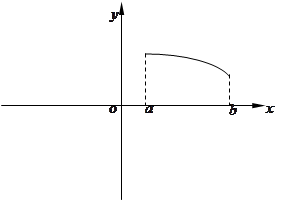
 (本题满分15分)如图:某污水处理厂要在一个矩形污水处理池
(本题满分15分)如图:某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道![]() ,
,![]() 是直角顶点)来处理污水,管道越短,铺设管道的成本越低WWW.K**S*858$$U.COM.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低WWW.K**S*858$$U.COM.设计要求管道的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米,![]() 米,记
米,记![]() .
.
(Ⅰ)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,
的函数,
并写出定义域;
(Ⅱ)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(Ⅲ)问:当![]() 取何值时,铺设管道的成本最低?并求出此时管道的长度.
取何值时,铺设管道的成本最低?并求出此时管道的长度.
(本题满分15分)
扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为![]() (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为![]() 平方米,且高度不低于
平方米,且高度不低于![]() 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为![]() (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段![]() 与两腰长的和)为
与两腰长的和)为![]() (米).
(米).
⑴求![]() 关于
关于![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过![]() 米,则其腰长
米,则其腰长![]() 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长![]() 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com