
题目列表(包括答案和解析)
已知函数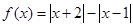 .
.
(1)试求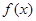 的值域;
的值域;
(2)设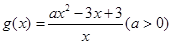 ,若对
,若对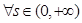 ,
,
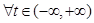 ,恒
,恒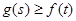 成立,试求实数
成立,试求实数 的取值范围
的取值范围
【解析】第一问利用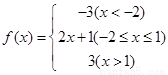
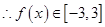
第二问中若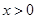 ,则
,则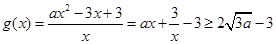 ,即当
,即当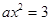 时,
时,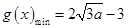 ,又由(Ⅰ)知
,又由(Ⅰ)知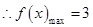
若对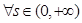 ,
,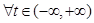 ,恒有
,恒有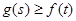 成立,即
成立,即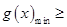
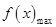 转化得到。
转化得到。
解:(1)函数可化为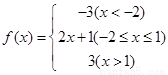 ,
,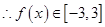 ……5分
……5分
(2) 若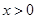 ,则
,则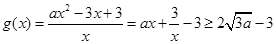 ,即当
,即当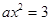 时,
时,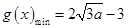 ,又由(Ⅰ)知
,又由(Ⅰ)知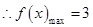 . …………8分
. …………8分
若对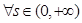 ,
,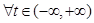 ,恒有
,恒有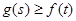 成立,即
成立,即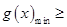
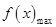 ,
,
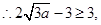
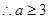 ,即
,即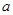 的取值范围是
的取值范围是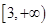
| a | x+1 |
| b |
| x |
|
|
| m |
| 2 |
| x2+ax+b |
| x |
| k |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com