
题目列表(包括答案和解析)
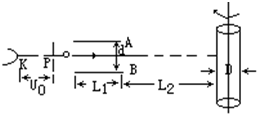
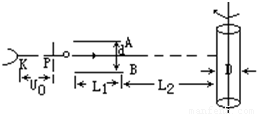
 (2005?闵行区二模)理论研究指出,简谐振动的振动位移X与时间t的关系图象(x-t)可以是一条余弦曲线,其函数表达式为:x=Acosωt,其中A是振幅,ω=2π/T.对于周期性变化的电压和电流的图象也可以是一条余弦曲线,其函数表达式类似.下图中从阴极K发射的电子经电势差U0=5000V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm、间距d=4cm的平行金属板A、B之间,在离金属板边缘L2=75cm处放置一个直径D=20cm、带有记录纸的圆筒.整个装置放在真空内,电子发射的初速度不计(见图).若在两金属板上交变电压以U2=1000cos2πt(V)的规律变化,并使圆筒绕中心轴按图示方向以n=2转/s匀速转动,电子质量为9.1×10-31kg,电子电量为1.6×10-19c求:
(2005?闵行区二模)理论研究指出,简谐振动的振动位移X与时间t的关系图象(x-t)可以是一条余弦曲线,其函数表达式为:x=Acosωt,其中A是振幅,ω=2π/T.对于周期性变化的电压和电流的图象也可以是一条余弦曲线,其函数表达式类似.下图中从阴极K发射的电子经电势差U0=5000V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm、间距d=4cm的平行金属板A、B之间,在离金属板边缘L2=75cm处放置一个直径D=20cm、带有记录纸的圆筒.整个装置放在真空内,电子发射的初速度不计(见图).若在两金属板上交变电压以U2=1000cos2πt(V)的规律变化,并使圆筒绕中心轴按图示方向以n=2转/s匀速转动,电子质量为9.1×10-31kg,电子电量为1.6×10-19c求:近期《科学》中文版的文章介绍了一种新技术——航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统.飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等.如图所示为飞缆系统的简化模型示意图,图中两个物体P,Q的质量分别为mP、mQ,柔性金属缆索长为l,外有绝缘层,系统在近地轨道做圆周运动,运动过程中Q距地面高为h.设缆索总保持指向地心,P的速度为vP.已知地球半径为R,地面的重力加速度为g.
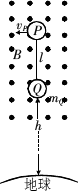
(1)飞缆系统在地磁场中运动,地磁场在缆索所在处的磁感应强度大小为B,方向垂直于纸面向外.设缆索中无电流,问:缆索P、Q哪端电势高;它们之间的电势差为多少.此问中可认为缆索各处的速度均近似等于vP,求P、Q两端的电势差;
(2)设缆索的电阻为R1,如果缆索两端物体P、Q通过周围的电离层放电形成电流,相应的电阻为R2,求缆索所受的安培力多大.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com