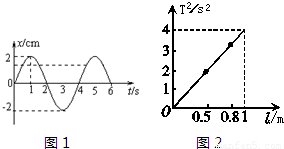
(1)一个质点做简谐运动的图象如图所示,质点振动频率为
0.25
0.25
Hz;在10s内质点经过的路程是
20
20
cm; t=4.5s时刻质点的位移是
cm;在5s末,速度为
零
零
(填零或最大),加速度
最大
最大
(填零或最大)
(2)在做“用单摆测定重力加速度”的实验中,某同学先测得摆线长为89.2cm,摆球的直径如图所示,然后用秒表记录了单摆做30次全振动.
①该单摆的摆长为
90.225
90.225
cm.
②如果该同学测得的g值偏大,可能的原因是
ABD
ABD
A.测摆长时记录的是摆球的直径
B.开始计时时,秒表过迟按下
C.摆线上端牢固地系于悬点,摆动中出现松动,使摆线长度增加了
D.实验中误将29次全振动数为30次
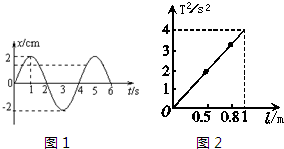
③为了提高实验精度,在实验中可改变几次摆长l,测出相应的周期T,从而得出一组对应的l与T的数值,再以l为横坐标,T
2为纵坐标,将所得数据连成直线如图所示,则测得的重力加速度g=
9.86
9.86
m/s
2(结果保留三位有效数字)
(3)另一同学在“用单摆测定重力加速度”的实验中,用的摆球密度不均匀,无法确定重心位置.他第一次量得悬线长为l
1(不计半径),测得周期为T
1;第二次量得悬线长为l
2,测得周期为T
2.根据上述数据,g=
.



 (1)一个质点做简谐运动的图象如图所示,质点振动频率为
(1)一个质点做简谐运动的图象如图所示,质点振动频率为