练习册

  • 练习册
  • 试题
    (2)如果记该考生答完4道题后所答对的题数为.求的分布列.数学期望与方差. 【查看更多】

     

    题目列表(包括答案和解析)

    2008年12月底，一考生参加某大学的自主招生考试，需进行书面测试，测试题中有4道题，每一道题能否正确做出是相互独立的，并且每一道题被该考生正确做出的概率都是，
    （1）若该考生至少正确做出3道题，才能通过书面测试这一关，求这名考生通过书面测试的概率；
    （2）如果记该考生答完4道题后所答对的题数为ξ，求ξ的分布列、数学期望与方差。

    查看答案和解析>>

     

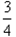    2008年12月底，一考生参加某大学的自主招生考试，需进行书面测试，测试题中有4道题，每一道题能否正确出是相互独立的，并且每一道题被该考生正确做出的概率都是。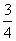

    （1）若该考生至少正确做出3道题，才能通过书面测试这一关，求这名考生通过书面测试的概率；

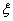    （2）如果记该考生答完4道题后所答对的题数为，求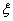的分布列、数学期望与方差。

     

     

     

     

     

    查看答案和解析>>

    （2011•洛阳一模）某班级举行一次知识竞赛，活动分为初赛和决赛，现将初赛成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
    分组（分数段） 频数（人数） 频率
    （60，70）
    8
    8
    		 0.16
    （70，80） 22
    0.44
    0.44
    （80，90） 14 0.28
    （90，100）
    6
    6
    0.12
    0.12
    合计 50
    1
    1
    （1）填充频率分布表中的空格（直接写出对应空格序号的答案，不必写过程）；
    （2）决赛规则如下：参加决赛的同学依次回答主持人的4道题，答对2道就终止答题，并获得一等奖；如果前三道题都答错，就不再回答第四题．某同学甲现已进入决赛（初赛80分以上，不含80分），每题答对的概率P的值恰好等于频率分布表中80分以上的频率值．
    ①求该同学答完3道题而获得一等奖的概率；
    ②记该同学决赛中答题的个数为ξ，求ξ的分布列．

    查看答案和解析>>

    某班级举行一次知识竞赛，活动分为初赛和决赛，现将初赛成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
    分组（分数段） 频数（人数） 频率
    （60，70） ______ 0.16
    （70，80） 22 ______
    （80，90） 14 0.28
    （90，100） ______ ______
    合计 50 ______
    （1）填充频率分布表中的空格（直接写出对应空格序号的答案，不必写过程）；
    （2）决赛规则如下：参加决赛的同学依次回答主持人的4道题，答对2道就终止答题，并获得一等奖；如果前三道题都答错，就不再回答第四题．某同学甲现已进入决赛（初赛80分以上，不含80分），每题答对的概率P的值恰好等于频率分布表中80分以上的频率值．
    ①求该同学答完3道题而获得一等奖的概率；
    ②记该同学决赛中答题的个数为ξ，求ξ的分布列．

    查看答案和解析>>

    某班级举行一次知识竞赛，活动分为初赛和决赛，现将初赛成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
    分组（分数段）频数（人数）频率
    （60，70）______0.16
    （70，80）22______
    （80，90）140.28
    （90，100）____________
    合计50______
    （1）填充频率分布表中的空格（直接写出对应空格序号的答案，不必写过程）；
    （2）决赛规则如下：参加决赛的同学依次回答主持人的4道题，答对2道就终止答题，并获得一等奖；如果前三道题都答错，就不再回答第四题．某同学甲现已进入决赛（初赛80分以上，不含80分），每题答对的概率P的值恰好等于频率分布表中80分以上的频率值．
    ①求该同学答完3道题而获得一等奖的概率；
    ②记该同学决赛中答题的个数为ξ，求ξ的分布列．

    查看答案和解析>>

     

    一、选择题（共60分）

    1―6DDBBAC  7―12DABCAC

    二、填空题：（本大题共5小题，每小题5分，共20分）

    13．3

    14．

    15．

    16．240

    三、解答题：本大题有6小题，共70分，解答应写出文字说明，证明过程或演算步骤。

    17．解：（1）

              1分

          

              5分

       （2）

              7分

           由余弦定理   9分

               10分

    18．（1）记“这名考生通过书面测试”为事件A，则这名考生至少正确做出3道题，即正确做出3道题或4道题，

           故   4分

       （2）由题意得的所有可能取值分别是0，1，2，3，4，且

     

          

          

              8分

          

           的分布列为：

          

    0

    1

    2

    3

    4

    P

              10分

              12分

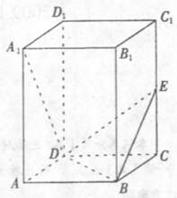
    19．解法一：（1）在直平行六面体ABCD―A1B1C1D1中，

          

           又

              4分

           又

       （2）如图，连B1C，则

           易证∽

           中点，

          

              8分

           取CD中点M，连BM， 则平面CC1D1D，

           作于N，连NB，由三垂线定理知：

           是二面角B―DE―C的平面角     10分

           在

          

           则二面角B―DE―C的大小为    12分

           解法二：（1）以D为坐标原点，射线DA为轴，建立如图所示坐标为

           依题设

          

          

           又

           平面BDE    6分

           8分

           由（1）知平面BDE的一个法向量为

           取DC中点M，则

          

          

           等于二面角B―DE―C的平面角    10分

              12分

    20．解：（1）由已知得   2分

           由

          

           递减

           在区间[-1，1]上的最大值为   4分

           又

          

           由题意得

           故为所求         6分

       （2）解：

          

               8分

           二次函数的判别式为：

          

           令

           令    10分

          

           为单调递增，极值点个数为0    11分

           当=0有两个不相等的实数根，根据极值点的定义，可知函数有两个极值点    12分

    21．解：（1）设

           化简得    3分

       （2）将    4分

           法一：两点不可能关于轴对称，

           的斜率必存在

           设直线DE的方程为

           由   5分

               6分

              7分

           且

              8分

           将代化入简得

              9分

           将，

           过定点（-1，-2）    10分

           将，

           过定点（1，2）即为A点，舍去     11分

               12分

           法二：设    （5分）

           则   6分

           同理

           由已知得   7分

           设直线DE的方程为

           得   9分

              10分

           即直线DE过定点（-1，-2）    12分

    22．解：（1）由    2分

           于是

           即    3分

           有   5分

              6分

       （2）由（1）得    7分

           而

          

                   

               10分

           当

           于是

           故命题得证     12分


    同步练习册答案