
题目列表(包括答案和解析)
(本小题满分12分)为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气的含药量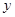 (毫克)与时间
(毫克)与时间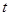 (小时)成正比.药物释放完毕后,
(小时)成正比.药物释放完毕后,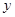 与
与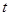 的函数关系式为
的函数关系式为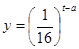 (
(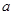 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
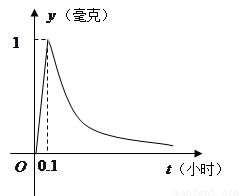
(1)求从药物释放开始,每立方米空气中的含药量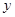 (毫克)与时间
(毫克)与时间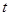 (小时)之间的函数关系式;(2)据测定,当空气中每立方米空气的含药量降到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到进教室?
(小时)之间的函数关系式;(2)据测定,当空气中每立方米空气的含药量降到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到进教室?
(2009宁夏海南卷理)(本小题满分12分)
某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
| 生产能力分组 |
|
|
|
|
|
| 人数 | 4 | 8 |
| 5 | 3 |
表2:
| 生产能力分组 |
|
|
|
|
| 人数 | 6 | y | 36 | 18 |
(i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)

(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)
(本小题满分12分)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段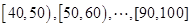 ,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(1)求70~80分数段的学生人数;
(2)估计这次考试中该学科的优分率(80分及以上为优分)
(3)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.[来源:学#科#网]
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
|
生产能力分组 |
|
|
|
|
|
|
人数 |
4 |
8 |
|
5 |
3 |
表2:
|
生产能力分组 |
|
|
|
|
|
人数 |
6 |
y |
36 |
18 |
(1)先确定 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)

(2)分别估计 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)
(本题满分12分)
为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为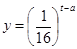 (a为常数),
(a为常数),
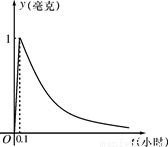
如图所示,根据图中提供的信息,回答下列问题:
(Ⅰ)从药物释放开始,求每立方米空气中的含药量
y(毫克)与时间t(小时)之间的函数关系式?
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到教室.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com