
题目列表(包括答案和解析)
(本小题满分13分)
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为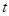 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若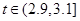 ,则该零件为优等品;若
,则该零件为优等品;若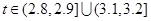 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
|
尺寸 |
|
|
|
|
|
|
|
甲机床零件频数 |
2 |
3 |
20 |
20 |
4 |
1 |
|
乙机床零件频数 |
3 |
5 |
17 |
13 |
8 |
4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元. 若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: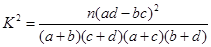 .
.
参考数据:
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
|
|
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
(本小题满分13分)
现有甲、乙两个项目,对甲项目投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为 、
、 、
、 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是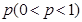 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为 ,对乙项目投资十万元,
,对乙项目投资十万元,  取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量 、
、 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求 、
、 的概率分布和数学期望
的概率分布和数学期望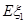 、
、 ;
;
(II)当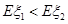 时,求
时,求 的取值范围.
的取值范围.
(本小题满分13分)
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
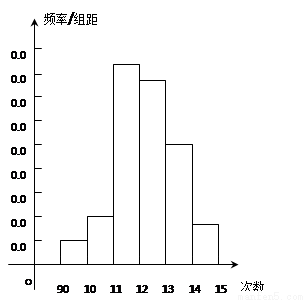
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(Ⅲ)在这次测试中,学生跳绳次数的中位数、众数各是是多少?(精确到0.1)
(2010福建理数)17.(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
(本小题满分13分)
某班名学生在2011年某次数学测试中,成绩全部介于80分与130分之间,将测试结果按如下方式分成五组,第一组[80,90);第二组[90,100)…第五组[120,130],下表是按上述分组方法得到的频率分布表:
| 分 组 | 频 数 | 频 率 |
| [80,90) | 0.04 | |
| [90,100) | 9 | |
| [100,110) | 0.38 | |
| [110,120) | 17 | 0.34 |
| [120,130] | 3 | 0.06 |
(Ⅰ) 求及分布表中的值;
(Ⅱ)校长决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一名学生被抽到的概率;
(Ⅲ)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为,求事件“”的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com