（1）有同学利用如图1的装置来验证力的平行四边形定则：在竖直木板上铺有白纸，固定两个光滑的滑轮A和B，将绳子打一个结点O，每个钩码的质量相等，当系统达到平衡时，根据钩码个数读出三根绳子的拉力T_OA、T_OB和T_OC，回答下列问题：
a改变钩码个数，实验能完成的是

A．钩码的个数N₁=N₂=2，N₃=4
B．钩码的个数N₁=N₃=3，N₂=4
C．钩码的个数N₁=N₂=N₃=4
D．钩码的个数N₁=3，N₂=4，N₃=5
b在拆下钩码和绳子前，应该做好三个方面的记录：；；
（2）如图2所示装置，在探究影响平行板电容器电容的因素实验中，①充好电的平行板电容器的极板A与一静电计相接，极板B接地．若极板B稍向上移动一点，由观察到的静电计指针变化分析平行板电容器电容变小结论的依据是
A．两极板间的电压不变，极板上的电量变大
B．两极板间的电压不变，极板上的电量变小
C．极板上的电量几乎不变，两极板间的电压变大
D．极板上的电量几乎不变，两极板间的电压变小
②如图3所示为电容式传感器构件的示意图，工作时动片（电极板A）沿平行于定片（电极板B）的方向发生一小段位移s，电容C便发生变化，通过测量电容C的变化情况就可以知道位移s．如果忽略极板的边缘效应，那么在图中，能正确反映电容C和位移s间函数关系的是．（选填选项前面的字母）

（3）某同学在探究影响单摆振动周期的因素时，针对自己考虑到的几个可能影响周期的物理量设计了实验方案，并认真进行了实验操作，取得了实验数据．他经过分析后，在实验误差范围内，找到了在摆角较小的情况下影响单摆周期的一个物理量，并通过作图象找到了单摆周期与这个物理量的明确的数量关系．该同学的实验数据记录如下：

摆长L/m 周期T/s 最大摆角θ/° 摆球种类及质量m/g		0.7000	0.7500	0.8000	0.8500	0.9000
钢球A 8.0	3.0	1.69	1.73	1.80	1.86	1.89
	9.0	1.68	1.74	1.79	1.85	1.90
钢球B 16.0	3.0	1.68	1.74	1.79	1.85	1.90
	9.0	1.69	1.73	1.80	1.85	1.89
铜球 20.0	3.0	1.68	1.74	1.80	1.85	1.90
	9.0	1.68	1.74	1.79	1.85	1.90
铝球 6.0	3.0	1.68	1.74	1.80	1.85	1.90
	9.0	1.69	1.74	1.80	1.86	1.91

①分析上面实验表格中的数据，你认为在摆角较小的情况下影响单摆周期的这个物理量是：．
②利用表中给出的数据，试在图4中坐标纸上画出T²与L的关系图线，该图线斜率k的表达式k=，k的数值为k=．利用图线斜率k表示重力加速度的表达式为g=（用字母表示）．

光电门传感器在很多实验中应用．光电门直接测量的物理量是．它能测量瞬时速度的原理是．
如图所示的实验装置中的横杆能够绕竖直轴旋转，在横杆的一端装有宽度为d=0.005m的竖直“挡光圆柱”．横杆在转动过程中，由于摩擦阻力的作用，横杆会越转越慢．某同学利用光电门研究“挡光圆柱”速度大小与横杆转动圈数n的关系．在一次实验中记录下横杆转动圈数n和每次挡光的时间t，并计算出“挡光圆柱”在该时刻的速度以及速度的平方（部分数据如表中所示）．请计算表中当n=5时，v²=m²/s²；如果继续测量“挡光圆柱”的速度，那么当n=15时，“挡光圆柱”的速度为m/s．则“挡光圆柱”速度大小与横杆转动圈数n的关系为． 

n	t（10-3s）	v=d/t（m/s）	v2（m2/s2）
1	2.778	1.80	3.24
2	2.826	…	3.13
3	2.877	…	3.02
4	2.931	…	2.91
5	2.988	…
6	3.049	…	2.69
7	3.113	…	2.58
8	3.181	…	2.47
9	3.255	…	2.36
10	3.333	…	2.25
…	…	…	…

（2005?南通一模）某同学采用如图1所示的电路测定电源电动势和内电阻，已知干电池的电动势约为1.5V，内阻约1Ω，电压表（0-3V 3kΩ），电流表（0-0.6A 1.0Ω），滑动变阻器有R₁（10Ω 2A）和R₂（100Ω 0.1A）各一只；
  
（1）实验中滑动变阻器应选用（选填R₁．R₂）
（2）在图2中用笔画线代替导线连接实验电路．
（3）在实验中测得多组电压和电流值，得到 如图3所示的U-I，由图可较准确求出电源电动势E=V，内阻r=Ω．

（2008?南通三模）（1）①如图游标卡尺的读数为_mm．②图中给出的是用螺旋测微器测量一金属薄板厚度时的示数，此读数应为mm．

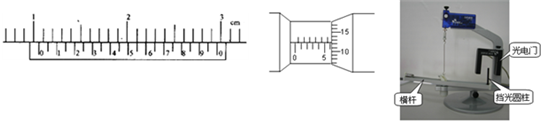
（2）如图所示的实验装置中的横杆能够绕竖直轴旋转，横杆在转动过程中，由于摩擦阻力的作用，横杆会越转越慢．在横杆的一端装有宽度为d=0.005m的竖直“挡光圆柱”，当“挡光圆柱”通过光电门时，光电门就记录挡光的时间间隔，“挡光圆柱”宽度与挡光时间之比，可以近似认为是“挡光圆柱”在该时刻的速度．横杆每转一圈，“挡光圆柱”通过

n	t（10-3s）	v=d/t（m/s）	v2（m2/s2）
1	2.778	1.80	3.24
2	2.826	…	3.13
3	2.877	…	3.02
4	2.931	…	2.91
5	2.988	…
6	3.049	…	2.69
7	3.113	…	2.58
8	3.181	…	2.47
9	3.255	…	2.36
10	3.333	…	2.25
…	…	…	…

光电门记录一次挡光时间．
在一次实验中记录下横杆转动圈数n和每次挡光的时间t，并计算出“挡光圆柱”在该时刻的速度以及速度的平方（部分数据如表中所示）．请计算表中当n=5时，v²=m²/s²；如果继续测量“挡光圆柱”的速度，那么当n=15时，“挡光圆柱”的速度为m/s．则“挡光圆柱”速度大小与横杆转动圈数n的关系为．

（2010?岳阳模拟）如图所示的实验装置中的横杆能够绕竖直轴旋转，横杆在转动过程中，由于摩擦阻力的作用，横杆会越转越慢．在横杆的一端装有宽度为d=0.005m的竖直“挡光圆柱”，当“挡光圆柱”通过光电门时，光电门就记录挡光的时间间隔，“挡光圆柱”宽度与挡光时间之比，可以近似认为是“挡光圆柱”在该时刻的速度．横杆每转一圈，“挡光圆柱”通过光电门记录一次挡光时间．

n	t（10-3s）	v= d t （m/s）	v2（m2/s2）
1	2.778	1.80	3.24
2	2.826	…	3.13
3	2.877	…	3.02
4	2.931	…	2.91
5	2.988	…
6	3.049	…	2.69
7	3.113	…	2.58
8	3.181	…	2.47
9	3.255	…	2.36
10	3.333	…	2.25
…	…	…	…

在一次实验中记录下横杆转动圈数n和每次挡光的时间t，并计算出“挡光圆柱”在该时刻的速度以及速度的平方（部分数据如表中所示）．请计算表中当n=5时，v²=m²/s²；如果继续测量“挡光圆柱”的速度，那么当n=15时，“挡光圆柱”的速度为m/s．则“挡光圆柱”速度大小与横杆转动圈数n的关系为．