
题目列表(包括答案和解析)
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点 、
、 ,点
,点 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到 倍后得到点
倍后得到点 满足
满足 .
.
(1) 求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)(理科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 ,又点
,又点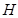 关于原点O的对称点为点
关于原点O的对称点为点 ,试问四点
,试问四点 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 (O为坐标原点),试判断点
(O为坐标原点),试判断点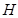 是否在曲线
是否在曲线 上,并说明理由.
上,并说明理由.
(本小题满分16分)
已知数列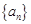 是各项均为正数的等差数列.
是各项均为正数的等差数列.
(1)若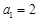 ,且
,且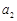 ,
,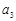 ,
,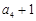 成等比数列,求数列
成等比数列,求数列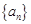 的通项公式
的通项公式 ;
;
(2)在(1)的条件下,数列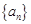 的前
的前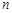 和为
和为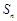 ,设
,设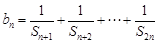 ,若对任意的
,若对任意的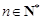 ,不等式
,不等式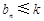 恒成立,求实数
恒成立,求实数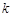 的最小值;
的最小值;
(3)若数列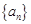 中有两项可以表示为某个整数
中有两项可以表示为某个整数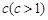 的不同次幂,求证:数列
的不同次幂,求证:数列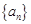 中存在无穷多项构成等比数列.
中存在无穷多项构成等比数列.
(本题满分16分)已知向量 ,
, =(1,2).
=(1,2).
(1)若 ,求tan
,求tan 的值; (2)若
的值; (2)若 ,
, ,求
,求 的值.
的值.
(本题满分16分)
函数f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线3x+y+2=0.
(1)求a,b的值; (2)求函数的极大值与极小值的差.
(本题16分,第(1)小题3分;第(2)小题5分;第(3)小题8分)
已知数列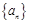 和
和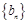 的通项分别为
的通项分别为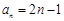 ,
,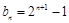 (
(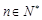 ),集合
),集合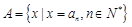 ,[来源:Zxxk.Com]
,[来源:Zxxk.Com]
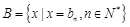 ,设
,设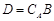 . 将集合
. 将集合 中元素从小到大依次排列,构成数列
中元素从小到大依次排列,构成数列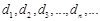 .
.
(1)写出 ;
;
(2)求数列 的前
的前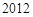 项的和;
项的和;
(3)是否存在这样的无穷等差数列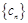 :使得
:使得 (
(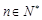 )?若存在,请写出一个这样的
)?若存在,请写出一个这样的
数列,并加以证明;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com