（本小题满分10分）已知：如图，⊙与轴交于C、D两点，圆心的坐标

为（1，0），⊙的半径为，过点C作⊙的切线交轴于点B（－4，0）

1.（1）求切线BC的解析式；

2.（2）若点P是第一象限内⊙上一点，过点P作⊙A的切线与直线BC相交于点G，

且∠CGP＝120°，求点的坐标；

3.（3）向左移动⊙（圆心始终保持在轴上），与直线BC交于E、F，在移动过程中是否存在点，使得△AEF是直角三角形？若存在，求出点 的坐标，若不存在，请说明理由．

（本小题满分10分）
在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：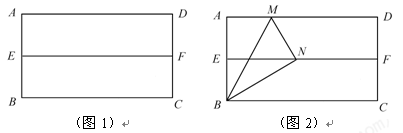

第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；
第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）
请解答以下问题：
【小题1】（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论．
【小题2】（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP ？

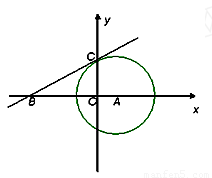
（本小题满分10分）已知：如图，⊙与轴交于C、D两点，圆心的坐标

为（1，0），⊙的半径为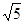，过点C作⊙的切线交轴于点B（－4，0）

1.（1）求切线BC的解析式；

2.（2）若点P是第一象限内⊙上一点，过点P作⊙A的切线与直线BC相交于点G，

且∠CGP＝120°，求点的坐标；

3.（3）向左移动⊙（圆心始终保持在轴上），与直线BC交于E、F，在移动过程中是否存在点，使得△AEF是直角三角形？若存在，求出点 的坐标，若不存在，请说明理由．