
题目列表(包括答案和解析)
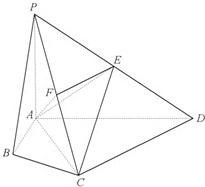 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.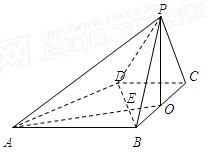 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E.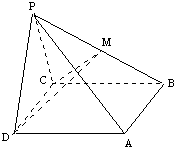 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ADC=60°,M为PB的中点,
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ADC=60°,M为PB的中点,(本小题满分12分)
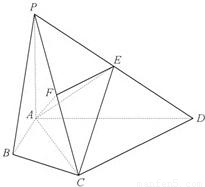
如图,已知四棱锥P—ABCD的底面是直角梯形,![]() ,AB=BC=PB=PC=2CD=2,侧面
,AB=BC=PB=PC=2CD=2,侧面![]() 底面ABCD,O是BC中点,AO交BD于E.
底面ABCD,O是BC中点,AO交BD于E.
(1)求证:![]() ;
;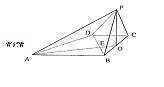 (2)求二面角
(2)求二面角![]() 的大小;
的大小;
(3)求证:平面![]() 平面PAB.
平面PAB.
1.解析:答案A.集合P表示正方形,集合Q表示圆面,作出它们的图形即可.
评析:利用二个集合间的几何意义借助数形结合思想,是本题考察的重点.
2.解析: .
.
答案:A.
评析:本题是考察二项式展开式的应用,难点是项数的舍弃.
3.解析:f(x)的图象向右平移 个单位,得sin[(x-
个单位,得sin[(x- )+
)+ ]=sinx,又g(x)=cos(x-
]=sinx,又g(x)=cos(x- =cos(
=cos( -x)=sinx.答案:D.
-x)=sinx.答案:D.
评析:本题是考察三角函数的等价变换与图象的平移.
4.答案A.解析:将三种抽样法的有关计算公式计算所得的概率都是 ,故选A.
,故选A.
(文)A .当函数的图像左右平移时,不改变函数的值域.
5.解析:.∵ 可视为曲线上两点
可视为曲线上两点 、
、 的斜率,作图易得
的斜率,作图易得 .选C.
.选C.
评析:本题是考察转化与数形结合的思想,解题的关键是将函数与不等式问题转化为解析几何问题.
6.解析:取△ABC为正三角形易得 =3.选B.
=3.选B.
评析:本题考查向量的有关知识,如果按常规方法就比较难处理,但是用特殊值的思想就比较容易处理,考查学生灵活处理问题的能力.
7.解析:易知 ,且当x∈
,且当x∈ 时,
时, 为增函数.又由
为增函数.又由 ,得
,得 ,故
,故  |,于是
|,于是 .选B.
.选B.
评析:本题考查运用奇函数、偶函数与增函数的概念与性质解决问题.
8.解析:显然S1是正确的.假设后三个数均未算错,则a1=8,a2=12,a3=16,a4=29,可知a22≠a ,显然S3=36≠8(1+q+q2),矛盾.只可能是S3算错了,此时由a2=12得
,显然S3=36≠8(1+q+q2),矛盾.只可能是S3算错了,此时由a2=12得 ,a3=18,a4=27,S4=S2+18+27=65,满足题设.选C.
,a3=18,a4=27,S4=S2+18+27=65,满足题设.选C.
评析:本题考查等比数列的基本概念与性质和学生推理的能力.
9.解析:答 由 的图象及
的图象及 的意义知,在x>0时,
的意义知,在x>0时, 为单调递增函数且
为单调递增函数且 <0;在x<0时,
<0;在x<0时, 为单调递减函数且
为单调递减函数且 <0.选D.
<0.选D.
评析:本题考查学生灵活运用导数知识与观察问题的能力.
10.解析:答⑴静放在点 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点 沿直线出发,经椭圆壁右顶点反弹后第一次回到点
沿直线出发,经椭圆壁右顶点反弹后第一次回到点 时,小球经过的路程是
时,小球经过的路程是 ,则选B;⑵静放在点
,则选B;⑵静放在点 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点 沿直线出发,经椭圆壁左顶点反弹后第一次回到点
沿直线出发,经椭圆壁左顶点反弹后第一次回到点 时,小球经过的路程是
时,小球经过的路程是 ,则选C;⑶静放在点
,则选C;⑶静放在点 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点 沿直线出发,经椭圆壁非左右顶点反弹后第一次回到点
沿直线出发,经椭圆壁非左右顶点反弹后第一次回到点 时,小球经过的路程是
时,小球经过的路程是 ,则选A.
,则选A.
于是三种情况均有可能,故选D.
评析:本题考察学生是否掌握光学的有关性质与解几相关的性质以及分类讨论的重要思想方法.
11.分析:解决数学问题的思维过程,一般总是从正面入手,即从已知条件出发,经过一系列的推理和运算,最后得到所要求的结论,但有时会遇到从正面不易入手的情况,这时可从反面去考虑.从反面考虑问题在集合中的运用主要就是运用补集思想.本题若直接求解,情形较复杂,也不容易得到正确结果,若我们先考虑其反面,再求其补集,就比较容易得到正确的解答.
解:由题知可解得A={y|y>a2+1或y<a}, B={y|2≤y≤4},我们不妨先考虑当A∩B=φ时a的范围.如图

由 ,得
,得
∴ 或
或 .
.
即A∩B=φ时a的范围为 或
或 .而A∩B≠φ时a的范围显然是其补集,从而所求范围为
.而A∩B≠φ时a的范围显然是其补集,从而所求范围为 .
.
评注:一般地,我们在解时,若正面情形较为复杂,我们就可以先考虑其反面,再利用其补集,求得其解,这就是“补集思想”.
解析:答:39.每个三棱锥中有三对异面直线,则异面直线的对数是3(C46-2)=39.
12.评析:本题把排列组合和立体几何挂起钩来,考生则必须对立体几何的有关知识有所了解和掌握.
13.解析:答 由 ,即
,即  ,得
,得 .
.
 ,
, .故
.故 =4.
=4.
评析:本题采用基本量法来作,但显然运算量会大上许多,本题可用特殊法处理.
14.解析:.设长分割成x列,宽分割成y行,共分割成z块,
则


z=x?y
当x=39,y=18时, .
.
评析:本题主要考查线性规划知识以及利用数形结合法解决问题,特别是已知区域求最优解是学生易错的地方.
15.解析:本题为开放题,只要写出一个正确的即可,如(2,1,-3,2).
评析:本题为开放题,考察学生对知识灵活处理问题的能力.
16.解析:



 …………………………
…………………………
当 >0时,
>0时,
 ,
,
解得 ,………………………………………………………………
,………………………………………………………………
从而,
 ,
,
T= ,最大值为5,最小值为-5;………………………………………………
,最大值为5,最小值为-5;………………………………………………
当m<0时, 解得 ,………………………………………………
,………………………………………………
从而, ,T=
,T= ,最大值为
,最大值为 ,
,
最小值为 .……………………………………………………………………
.……………………………………………………………………
评析:本题考查三角函数的运算.考查的知识点有和差化积、周期与三角函数
值域的求法、分类讨论的思想方法.近几年三角运算一直是考试所要求的基本题型之一,本题就是基于这一要求而制定的.
17.解析:(1) 由题意可知 x甲 ~ B(5, p1),
∴ Dx甲 = 5p1 (1-p1) = Þ p12-p1 + = 0 Þ p1 = .2分;又 ?= 6,∴ p2 = . 3分
(2) 两类情况:共击中3次概率
C ( ) 2 ( ) 0×C ( ) 1 ( ) 1 + C ( ) 1 ( ) 1×C ( ) 2 ( ) 0 = ;
共击中4次概率C ( ) 2 ( ) 0×C ( ) 2 ( ) 0 = . 6分
所求概率为 + = . 8分
(3) 设事件A, B分别表示甲、乙能击中.∵ A, B互相独立(9分),∴ P(`A?`B ) = P(`A ) P(`B ) = (1-P(A) )(1-P(B) ) = (1-p1)(1-p2) = ×= (11分),∴ 1-P(`A?`B ) = 为所求概率. 12分
评析:这一类型的试题在连续几年的新课程卷都出现了,重点考查了分类讨论的数学思想,体现了《考试说明》所要求的创新意识和实践能力以及运用数学知识解决实际问题的能力.该题仍然是常规题,要求考生耐心细致,审题能力较强,并善于利用材料进行分析说明.

18.方法一:(I)证明: ,又
,又 平面
平面 平面ABCD,平面
平面ABCD,平面 平面ABCD=BC,
平面ABCD=BC, 平面ABCD ……2分
平面ABCD ……2分
在梯形ABCD中,可得
 ,即
,即
 在平面ABCD内的射影为AO,
在平面ABCD内的射影为AO, ……4分
……4分
(II)解: ,且平面
,且平面 平面ABCD
平面ABCD
 平面PBC,
平面PBC,  平面PBC,
平面PBC,
 为二面角P―DC―B的平面角 ……6分
为二面角P―DC―B的平面角 ……6分
 是等边三角形
是等边三角形 即二面角P―DC―B的大小为
即二面角P―DC―B的大小为 …8分
…8分
(III)证明:取PB的中点N,连结CN, ①
①
 ,且平面
,且平面 平面ABCD,
平面ABCD, 平面PBC ……10分
平面PBC ……10分
 平面PAB
平面PAB  平面
平面 平面PAB ②
平面PAB ②
由①、②知 平面PAB…………..10分
平面PAB…………..10分
连结DM、MN,则由MN//AB//CD, ,
,
得四边形MNCD为平行四边形, ,
, 平面PAB.
平面PAB.
 平面PAD
平面PAD  平面
平面 平面PAB ……………….12分
平面PAB ……………….12分
方法二:取BC的中点O,因为 是等边三角形,
是等边三角形,
由侧面 底面ABCD 得
底面ABCD 得 底面ABCD ……1分
底面ABCD ……1分
以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O―xyz……2分

(I)证明: ,则在直角梯形中,
,则在直角梯形中,
在等边三角形PBC中, ……3分
……3分



 ,即
,即 …4分
…4分
(II)解:取PC中点N,则

 平面PDC,显然
平面PDC,显然 ,且
,且 平面ABCD
平面ABCD
 所夹角等于所求二面角的平面角 ……6分
所夹角等于所求二面角的平面角 ……6分

 ,
, 二面角
二面角 的大小为
的大小为 ……8分
……8分
(III)证明:取PA的中点M,连结DM,则M的坐标为
又 ……10分
……10分
 ,
,
 即
即
 平面PAB,
平面PAB, 平面
平面 平面PAB ……12分
平面PAB ……12分
评析:本题考察的空间中的线线关系、面面关系以及二面角的求法关系是立体几
何中的最主要关系,熟悉它们的判定和性质是高考复习的重点,本题重在考查学生的运算能力、空间想象能力.
19.解(1)∵ ,
, ,∴
,∴ ,
, .
.
∵ =0,∴(
=0,∴( .……………………4分
.……………………4分
(2)由(1)知,双曲线的方程可设为 ,渐近线方程为
,渐近线方程为 .…5分
.…5分
设P1(x1,2x1),P2(x2,-2x2),P(x,y).
∵ ,∴
,∴ . ∵
. ∵ ,∴
,∴ ………8分
………8分
∵点P在双曲线上,∴ .
.
化简得, .∴
.∴ .∴
.∴  .∴双曲线的方程为
.∴双曲线的方程为 …12分
…12分
评析:本题考查向量与双曲线的有关内容.近几年来向量与其他知识互相渗透成为一种时尚,基于此特命此题.本题考查学生运用圆锥曲线定义灵活解题的能力、向量知识、运算能力.
当 时,
时,  ①
①
 ②
②
由①-②得,  ………(3分)
………(3分)
∵ ∴
∴ 即
即 ∴
∴ 适合上式,
适合上式,
(2)由(1)知,  ③
③
当 时,
时,  ④
④
由③-④得,

 ……(8分)
……(8分)
∵ , ∴
, ∴ , 数列
, 数列 是等差数列,首项为1,公差为1, 可得
是等差数列,首项为1,公差为1, 可得
 …(10分)
…(10分)
(3)
∵ , ∴
, ∴ ………(11分)
………(11分)
∴ ,
,
∴
 ⑤………(12分)
⑤………(12分)
当 时, ⑤式即为
时, ⑤式即为
 ⑥
⑥
依题意, ⑥式对 都成立, 当
都成立, 当 时,
时,
⑤式即为
 ⑦依题意, ⑦式对
⑦依题意, ⑦式对 都成立,
都成立,
∴ ………(13分) ∴
………(13分) ∴ 又
又 ,
,
21.解:(1)当x∈[-1,0]时,2-x∈[2,3],f(x)=g(2-x)=
-2ax+4x3;当x∈ 时,f(x)=f(-x)=2ax-4x3,
时,f(x)=f(-x)=2ax-4x3,
∴ ………………………………………4分
………………………………………4分
(2)由题设知, >0对x∈
>0对x∈ 恒成立,即
恒成立,即 恒成立,于是,a>6x2,从而a>(6x2)max=6.………………………8分
恒成立,于是,a>6x2,从而a>(6x2)max=6.………………………8分
(3)因f(x)为偶函数,故只需研究函数f(x)=2ax-4x3在x∈ 的最大值.
的最大值.
令 =
= .…10分 若
.…10分 若 ∈
∈ ,即0<a≤6,则
,即0<a≤6,则
 ,
,
故此时不存在符合题意的 ;
;
若 >1,即a>6,则
>1,即a>6,则 在
在 上为增函数,于是
上为增函数,于是 .
.
令
评析:本题通过函数的知识来切入到导数,是在这两个重要知识的交汇处命题,意在考查学生的逻辑思维能力与推理能力,函数及导数的应用是数学的难点,也是考得最热的话题之一,也是本套试卷的把关题,对学生的要求较高.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com