练习册

  • 练习册
  • 试题
    解:(1) =2+sinx-cos2x-1+sinx=sin2x+2sinx (1) 设函数y=f (x)的图象上任一点M(x0,y0)关于原点的对称点为N(x,y) 则x0= -x,y0= -y ∵点M在函数y=f (x)的图象上 ,即y= -sin2x+2sinx ∴函数g(x)的解析式为g(x)= -sin2x+2sinx (3)设sinx=t,(-1≤t≤1) 则有 ① 当时.h(t)=4t+1在[-1,1]上是增函数.∴λ= -1 ② 当时.对称轴方程为直线. ⅰ) 时..解得 ⅱ)当时.,解得 综上.. 已知向量满足.且.其中. (1)试用k表示.并求出的最大值及此时的夹角的值. (2)当取得最大值时.求实数.使的值最小.并对这一结果作出几何解释 (1) .此时 即的最大值为.此时的夹角的值为. (2)由题意.故 ∴当时.的值最小.此时 即当时.的值最小. 如图.在△ABC中.点M为BC的中点.A.B.C三点坐标分别为. .点N在AC上.且.AM与BN的交点为P.求: (1)点P分向量所成的比的值, (2)P点坐标. 解:(1)∵A.B.C三点坐标分别为.. 由于M为BC中点.可得M点的坐标为(1.1) ---1分 由可得N点的坐标为 --1分 又由可得P点的坐标为(. -1分 从而得. . -----2分 ∵与共线 故有))-((＝0 -2分 解之得4 -----2分 ∴点P的坐标为(.) 正六边形的中心为点为平面上异于的任意一点. 且 .则实数的值为C A. B. C. D.不确定 已知的面积满足.且 (1)求函数的最大值, (2)若.求的取值范围. 解:(1)如图:由 得. ∵ ∴而 ∴ ---------------- 2分 ∵ ∵ ∴ 从而 ∴ ----------- 5分 ∵ ∴当时.有最大值 ------- 7分 (2)∵ -------- 9分 ∴ ------------- 10分 ∴ ------------- 11分 ∵ ∴ ∴ 故的取值范围为 ------------- 13分 已知的面积满足.且 (1)求函数的值域, (2)若.求的最大值. 【查看更多】

     

    题目列表(包括答案和解析)

    已知 S=1+（1+3）+（1+3+5）+（1+3+5+7）+…+（1+3+5+…+199）
    （Ⅰ）下面给出求S的算法，请将空白部分补充完整；
    （Ⅱ）请将求S的流程图补充完整，内容直接填在程序框图中；
    解：（Ⅰ）算法分析：（1）S=0，T=0，i=1；
    （2）将T+2i-1赋值给T，将S+T赋值给S；
    （3）将
     
    赋值给i；
    （4）
     
    ；
    （5）输出S，结束运算．
    （Ⅱ）流程图：
    精英家教网

    查看答案和解析>>

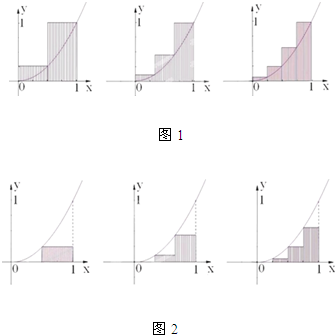    为了求函数y=x2，函数x=1，x轴围成的曲边三角形的面积S，古人想出了两种方案求其近似解（如图）：第一次将区间[0，1]二等分，求出阴影部分矩形面积，记为S2；第二次将区间[0，1]三等分，求出阴影部分矩形面积，记为S3；第三次将区间[0，1]四等分，求出S4…依此类推，记图1中Sn=an，图2中Sn=bn，其中n≥2．
    （1）求a2，a3，a4；
    （2）求an的通项公式，并证明an＞
    1
    3
    ；
    （3）求bn的通项公式，类比第②步，猜想bn的取值范围．并由此推出S的值（只需直接写出bn的范围与S的值，无须证明）．
    参考公式：12+22+32+…+(n-1)2+n2=
    1
    6
    n(n+1)(2n+1)    ．

    查看答案和解析>>

    设函数，其中 w.w.w.k.s.5.u.c.o.m    

    （1）解不等式  （2）求的取值范围，使在区间上是单调减函数。

    查看答案和解析>>

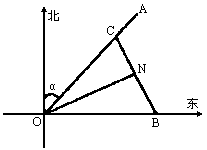
    如图，一载着重危病人的火车从O地出发，沿射线OA行驶，其中tanα＝，在距离O地5a(a为正数)公里北偏东β角的N处有一位医学专家，其中sinβ＝，现110指挥部紧急征调离O地正东p公里的B处的救护车赶往N处载上医学专家全速追赶乘有危重病人的火车，并在C处相遇，经测算当两车行驶的路线与OB围成的三角形OBC面积最小时，抢救最及时．

    (1)求S关于p的函数关系；

    (2)当p为何值时，抢救最及时．

    查看答案和解析>>

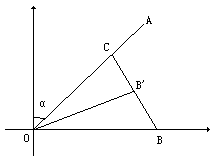
    如图，一载着重危病人的火车从O地出发，沿射线OA行驶，其中tanα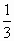＝，在距离O地5a(a为正数)公里北偏东β角的N处住有一位医学专家，其中sinβ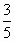＝，现110指挥部紧急征调离O地正东p公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车，并在C处相遇，经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时，抢救最及时，

    (1)求S关于p的函数关系；

    (2)当p为何值时，抢救最及时．

    查看答案和解析>>


    同步练习册答案