
题目列表(包括答案和解析)
求圆心在直线y=-2x上,并且经过点A(2,-1),与直线x+y=1相切的圆的方程.
【解析】利用圆心和半径表示圆的方程,首先
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2)
∴r=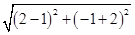 =
=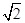 ,
,
故所求圆的方程为: +
+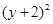 =2
=2
解:法一:
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2) ……………………8分
∴r=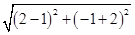 =
=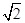 ,
………………………10分
,
………………………10分
故所求圆的方程为: +
+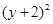 =2
………………………12分
=2
………………………12分
法二:由条件设所求圆的方程为: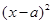 +
+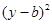 =
=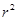
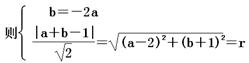 , ………………………6分
, ………………………6分
解得a=1,b=-2, 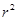 =2
………………………10分
=2
………………………10分
所求圆的方程为: +
+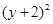 =2
………………………12分
=2
………………………12分
其它方法相应给分
已知函数f(x)(x∈R)满足f(x)=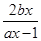 ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1=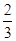 ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)=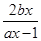 ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即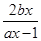 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)=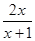 .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
=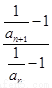 =
=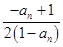 =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1=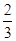 ,∴b1=
,∴b1=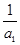 -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an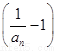 =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn=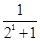 +
+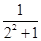 +…+
+…+ <
<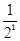 +
+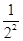 +…+
+…+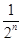
=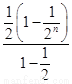 =1-
=1-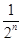 <1(n∈N*).
<1(n∈N*).
已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。第一问,利用函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中设切点为(x0,x03-3x0),因为过点A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分离参数∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函数求导数,判定单调性,从而得到要是有三解,则需要满足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依题意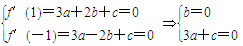
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)设切点为(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0)
又切线过点A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
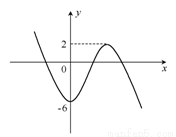
令g(x)=-2x3+6x2-6
则g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
∴g(x)在(-∞,0)单调递减,(0,2)单调递增,(2,+∞)单调递减.
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当-6<m<2时,m=-2x3+6x2-6有三解,
所以m的取值范围是(-6,2).
已知sina= ,aÎ(
,aÎ( ,p),cosb=-
,p),cosb=- ,b是第三象限的角.
,b是第三象限的角.
⑴ 求cos(a-b)的值;
⑵ 求sin(a+b)的值;
⑶ 求tan2a的值.
【解析】第一问中∵ aÎ( ,p),∴ cosa=-
,p),∴ cosa=-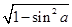 =-
=-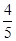 , ∵ b是第三象限的角,
, ∵ b是第三象限的角,
∴ sinb=- =-
=- ,
,
cos(a-b)=cosa·cosb+sina·sinb =(-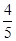 )×(-
)×(- )+
)+ ×(-
×(- )=-
)=-
⑵ 中sin(a+b)=sina·cosb+cosa·sinb = ×(-
×(- )+(-
)+(-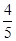 )×(-
)×(- )=
)=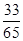 ⑶ 利用二倍角的正切公式得到。∵tana=
⑶ 利用二倍角的正切公式得到。∵tana= =-
=-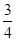 ∴tan2a=
∴tan2a= =
= =-
=-
解∵ aÎ( ,p),∴ cosa=-
,p),∴ cosa=-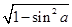 =-
=-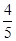 , …………1分
, …………1分
∵ b是第三象限的角,∴ sinb=- =-
=- , ………2分
, ………2分
⑴ cos(a-b)=cosa·cosb+sina·sinb …………3分
=(-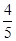 )×(-
)×(- )+
)+ ×(-
×(- )=-
)=- ………………5分
………………5分
⑵ sin(a+b)=sina·cosb+cosa·sinb ……………………6分
= ×(-
×(- )+(-
)+(-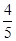 )×(-
)×(- )=
)=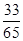 …………………8分
…………………8分
⑶ ∵tana= =-
=-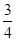 …………………9分
…………………9分
∴tan2a= ………………10分
………………10分
= =-
=-
设集合A={x|2x2+3px+2=0},B={x|2x2+x+q=0},其中p,q,x∈R.当A∩B={![]() }时,求p的值和A∪B.
}时,求p的值和A∪B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com