
题目列表(包括答案和解析)
若对任意![]() ,(
,(![]() )有唯一确定的
)有唯一确定的![]() 与之对应,则称
与之对应,则称![]() 为关于
为关于![]() 的二元函数。现定义满足下列性质的二元函数
的二元函数。现定义满足下列性质的二元函数![]() 为关于实数
为关于实数![]() 的广义“距离”:
的广义“距离”:
(1)非负性:![]() ,当且仅当
,当且仅当![]() 时取等号;
时取等号;
(2)对称性:![]() ;
;
(3)三角形不等式:![]() 对任意的实数
对任意的实数![]() 均成立.
均成立.
今给出三个二元函数,请选出所有能够成为关于![]() 的广义“距离”的序号:
的广义“距离”的序号:
①![]() ;②
;②![]() ;③
;③![]() ._________________.
._________________.
若对任意![]() ,(
,(![]() )有唯一确定的
)有唯一确定的![]() 与之对应,则称
与之对应,则称![]() 为关于
为关于![]() 的二元函数。现定义满足下列性质的二元函数
的二元函数。现定义满足下列性质的二元函数![]() 为关于实数
为关于实数![]() 的广义“距离”: (1)非负性:
的广义“距离”: (1)非负性:![]() ,当且仅当
,当且仅当![]() 时取等号; (2)对称性:
时取等号; (2)对称性:![]() ; (3)三角形不等式:
; (3)三角形不等式:![]() 对任意的实数
对任意的实数![]() 均成立.今给出三个二元函数,请选出所有能够成为关于
均成立.今给出三个二元函数,请选出所有能够成为关于![]() 的广义“距离”的序号:①
的广义“距离”的序号:①![]() ;②
;②![]() ;③
;③![]() .________.
.________.
若对任意![]() 有唯一确定的
有唯一确定的![]() 与之对应,则称
与之对应,则称![]() 为关于x,y的二元函数,现定义满足下列性质的
为关于x,y的二元函数,现定义满足下列性质的![]() 为关于实数x,y的广义“距离”:
为关于实数x,y的广义“距离”:
(1)非负性:![]() ,当且仅当x=y时取等号;
,当且仅当x=y时取等号;
(2)对称性:![]()
(3)三角形不等式:![]() 对任意的
对任意的
实数z均成立。
给出三个二元函数:①![]() ②
②![]()
③![]() 则所有能够成为关于x,y的广义“距离”的序号为 。
则所有能够成为关于x,y的广义“距离”的序号为 。
若对任意![]() 有唯一确定的
有唯一确定的![]() 与之对应,则称
与之对应,则称![]() 为关于x,y的二元函数,现定义满足下列性质的
为关于x,y的二元函数,现定义满足下列性质的![]() 为关于实数x,y的广义“距离”:
为关于实数x,y的广义“距离”:
(1)非负性:![]() ,当且仅当x=y时取等号;
,当且仅当x=y时取等号;
(2)对称性:![]()
给出三个二元函数:
①![]() ②
②![]() ③
③![]()
则所有能够成为关于x,y的广义“距离”的序号为 。
若对任意 ,
, ,(
,( 、
、 )有唯一确定的
)有唯一确定的 与之对应,称
与之对应,称 为关于
为关于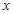 、
、 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数 为关于实数
为关于实数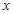 、
、 的广义“距离”:
的广义“距离”:
(1)非负性: ,当且仅当
,当且仅当 时取等号;
时取等号;
(2)对称性: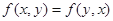 ;
;
(3)三角形不等式: 对任意的实数z均成立.
对任意的实数z均成立.
今给出四个二元函数:① ;②
;② ;③
;③ ;
;
④ .能够成为关于的
.能够成为关于的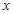 、
、 的广义“距离”的函数的所有序号是( )
的广义“距离”的函数的所有序号是( )
A. ① B. ② C. ③ D. ④
一、CABCB BDADD AC
二、13. 0.1;14. ;15. 36;16.存在,通项公式
;15. 36;16.存在,通项公式 。
。
三、
17.解:(1)依题意得:

得: ,
,
所以: ,即
,即 ,………………………………4分
,………………………………4分
|