练习册

  • 练习册
  • 试题
    将个正整数填入个方格中.使得每列.每条对角线上的数的和相等.这个正方形就叫做n阶幻方.如右图,就是一个3阶幻方.定义为n阶幻方对角线上数的和.例如,那么= 【查看更多】

     

    题目列表(包括答案和解析)

     将连续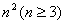个正整数填入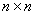的方格中，使其每行、每列、每条对角线上的各数

    8

    3

    4

    1

    5

    9

    6

    7

    2

    之和都相等，这个正方形叫做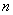阶幻方数阵，记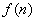为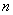阶幻方数阵对角线上

    各数之和，如图就是一个3阶幻方数阵，可知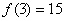。若将等差数列3，4，5，6，的前16 项填入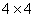方格中，可得到一个4阶幻方数阵，则  （     ）

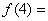     A．44         B．42          C．40        D．36

     

    查看答案和解析>>

    将n2(n≥3)个正整数1,2,3，…，n2填入n×n方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记f(n)为n阶幻方对角线上数的和。如下表所示

    8

    1

    6

    3

    5

    7

    4

    9

    2

     

    就是一个3阶幻方，可知f(3)＝15，则f(n)＝                       (　　)

    A. n(n2＋1)        B.  n2(n＋1)－3    C .n2(n2＋1)        D．n(n2＋1)

     

    查看答案和解析>>

    将n2(n≥3)个正整数1,2,3，…，n2填入n×n方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记f(n)为n阶幻方对角线上数的和。如下表所示

    8
    		1
    		6
    3
    		5
    		7
    4
    		9
    		2
     
    就是一个3阶幻方，可知f(3)＝15，则f(n)＝                       (　　)
    A．n(n2＋1)B．n2(n＋1)－3C．n2(n2＋1) D．n(n2＋1)

    查看答案和解析>>

    将n2(n≥3)个正整数1,2,3，…，n2填入n×n方格中，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n阶幻方，记f(n)为n阶幻方对角线上数的和。如下表所示
    8
    		1
    		6
    3
    		5
    		7
    4
    		9
    		2
     
    就是一个3阶幻方，可知f(3)＝15，则f(n)＝                       (　　)
    A．n(n2＋1)B．n2(n＋1)－3C．n2(n2＋1) D．n(n2＋1)

    查看答案和解析>>

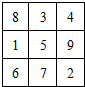    精英家教网将连续n2（n≥3）个正整数填入n×n方格中，使其每行．每列．每条对角线上的数的和都相等，这个正方形叫做n阶幻方数阵．记f（n）为n阶幻方数阵对角线上数的和，如右图就是一个3阶幻方数阵，可知f（3）=15．若将等差数列：3，4，5，6，…的前16项填入4×4方格中，可得到一个4阶幻方数阵，则其对角线上的和f（4）等于（　　）
    A、44B、42C、40D、36

    查看答案和解析>>


    同步练习册答案