
题目列表(包括答案和解析)
 (2010?云南模拟)如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B=
(2010?云南模拟)如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B=
|
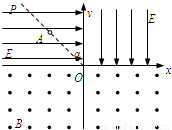 如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B=
如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B= .
. 如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B=
如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B=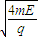 .
. 。
。
如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E,而x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角![]() ,一带正电的粒子从OP直线上某点A(—L,L)处由静止释放,重力不计,设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有
,一带正电的粒子从OP直线上某点A(—L,L)处由静止释放,重力不计,设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有![]()
(1)求粒子进入磁场时与x轴交点处的横坐标;
(2)求粒子进入磁场时速度方向与x轴正方向的夹角;
 (3)如果在OP直线上各点释放许多个上述带电粒子(粒子间的相互作用力不计),试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线。(提示:写出圆心点坐标x、y的函数关系)
(3)如果在OP直线上各点释放许多个上述带电粒子(粒子间的相互作用力不计),试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线。(提示:写出圆心点坐标x、y的函数关系)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com