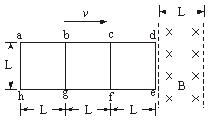
有一种“双聚焦分析器”质谱仪,工作原理如图所示.加速电场的电压为U,静电分析器中有辐向会聚电场,即与圆心O
1等距各点的电场强度大小相同,方向沿径向指向圆心O
1;磁分析器中以O
2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,其左边界与静电分析器的右边界平行.由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的电场方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器.而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器.测量出Q点与圆心O
2的距离为d,位于Q点正下方的收集器入口离Q点的距离为
.(题中的U、m、q、R、d都为已知量)
(1)求静电分析器中离子运动轨迹处电场强度E的大小;
(2)求磁分析器中磁感应强度B的大小;
(3)现将离子换成质量为4m,电荷量仍为q的另一种正离子,其它条件不变.磁分析器空间足够大,离子不会从圆弧边界射出,收集器的位置可以沿水平方向左右移动,要使此时射出磁分析器的离子仍能进入收集器,求收集器水平移动的距离.

 如图所示,水平固定放置的平行金属板M、N,两板间的距离为d,在两板的中心(即到上、下板距离相等,到板左、右端距离相等)有一悬点O,系有一长r=
如图所示,水平固定放置的平行金属板M、N,两板间的距离为d,在两板的中心(即到上、下板距离相等,到板左、右端距离相等)有一悬点O,系有一长r= 有一匀强磁场分布在以O为中心的一个圆形区域内,磁场方向垂直于xy平面(磁场未画出).某时刻起一个质量为m、电荷量为+q的带电粒子,由原点O开始运动,初速为v,方向沿x轴正方向.最终粒子到达y轴上的P点,此时速度方向与y轴的夹角为30°,已知OP的距离为L,如图所示.不计重力的影响.
有一匀强磁场分布在以O为中心的一个圆形区域内,磁场方向垂直于xy平面(磁场未画出).某时刻起一个质量为m、电荷量为+q的带电粒子,由原点O开始运动,初速为v,方向沿x轴正方向.最终粒子到达y轴上的P点,此时速度方向与y轴的夹角为30°,已知OP的距离为L,如图所示.不计重力的影响.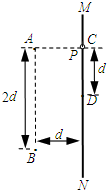 如图所示,两个带等量异种电荷的点电荷,电荷量均为 Q,固定于同一条竖直线上的 A、B 两点处,其中 A 处的电荷带正电,B 处的电荷带负电,A、B 相距为2d.MN 是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球 P,质量为 m、电荷量为+q (可视为点电荷),现将小球 P 从与点电荷 A 等高的 C 处由静止释放,小球 P 向下运动到与 C点距离为 d 的 D 点时,速度为 v.已知 MN 与 AB 之间的距离为 d,静电力常量为 k,重力加速度为 g,若取无限远处的电势为零,试求:
如图所示,两个带等量异种电荷的点电荷,电荷量均为 Q,固定于同一条竖直线上的 A、B 两点处,其中 A 处的电荷带正电,B 处的电荷带负电,A、B 相距为2d.MN 是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球 P,质量为 m、电荷量为+q (可视为点电荷),现将小球 P 从与点电荷 A 等高的 C 处由静止释放,小球 P 向下运动到与 C点距离为 d 的 D 点时,速度为 v.已知 MN 与 AB 之间的距离为 d,静电力常量为 k,重力加速度为 g,若取无限远处的电势为零,试求: 有一种“双聚焦分析器”质谱仪,工作原理如图所示.加速电场的电压为U,静电分析器中有辐向会聚电场,即与圆心O1等距各点的电场强度大小相同,方向沿径向指向圆心O1;磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,其左边界与静电分析器的右边界平行.由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的电场方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器.而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器.测量出Q点与圆心O2的距离为d,位于Q点正下方的收集器入口离Q点的距离为
有一种“双聚焦分析器”质谱仪,工作原理如图所示.加速电场的电压为U,静电分析器中有辐向会聚电场,即与圆心O1等距各点的电场强度大小相同,方向沿径向指向圆心O1;磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,其左边界与静电分析器的右边界平行.由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的电场方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器.而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器.测量出Q点与圆心O2的距离为d,位于Q点正下方的收集器入口离Q点的距离为