练习册

  • 练习册
  • 试题
    a＝-0.1 练习2 【查看更多】

     

    题目列表(包括答案和解析)

    下面是小明课后练习中的一道题：

    计算：(－3x2)(2x3＋x2－1)．

    解：(－3x2)(2x3＋x2－1)

    ＝(－3x2)·2x3＋(－3x2)·x2

    ＝－6x5－3x4．

    请你来做“小老师”，检查一下小明的解法是否正确；若不正确，请指出错在哪里，并给出正确的解法．

    查看答案和解析>>

    下面是一名学生所做的4道练习题：

    ①(－3)0＝1；

    ②a3＋a3＝a6；

    ③4m－4＝；

    ④(xy2)3＝x3y6，他做对的个数是

    [　　]

    A．0

    B．1

    C．2

    D．3

    查看答案和解析>>

    阅读下面内容并完成后面的练习：

    因为(x＋1)(x＋2)＝x2＋3x＋2，所以x2＋3x＋2＝(x＋1)(x＋2)；

    因为(x－1)(x－2)＝x2－3x＋2，所以x2－3x＋2＝(x－1)(x－2)；

    因为(x－1)(x＋2)＝x2＋x－2，所以x2＋x－2＝(x－1)(x＋2)；

    因为(x＋1)(x－2)＝x2－x－2，所以x2－x－2＝(x＋1)(x－2)；

    因为(x＋a)(x＋b)＝________，

    所以________＝(x＋a)(x＋b)．

    请你根据以上各式找出规律，并对下列多项式进行因式分解．

    (1)x2＋6x＋5；

    (2)a2－11a＋24；

    (3)m2n2＋14mn－32．

    查看答案和解析>>

    如图，排球运动员站在点O处练习发球，将球从O点正上方2 m的A处发出，把球看成点，其运行的高度y(m)与运行的水平距离x(m)满足关系式y＝a(x－6)2＋h．已知球网与O点的水平距离为9 m，高度为2.43 m，球场的边界距O点的水平距离为18 m．

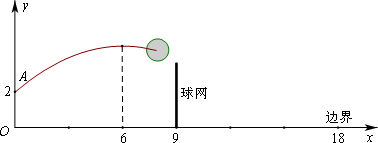
    (1)当h＝2.6时，求y与x的关系式(不要求写出自变量x的取值范围)

    (2)当h＝2.6时，球能否越过球网？球会不会出界？请说明理由；

    (3)若球一定能越过球网，又不出边界，求h的取值范围．

    查看答案和解析>>

    王老师要求学生进行编题，进行解题训练，其中小聪同学编的练习题是：

    设＝3，方程的两个实数根是，，求的值。

    小明同学对这道题的解答过程是：

    解：∵＝3

    ∴ 已知方程是

    又∵ +＝3，－＝3

    ∴ ＝

    即 ＝1。

    (1）请你针对以上的练习题和解答的正误作出判断，再简述理由；

    (2）请你只对小聪同学所编的练习题中的另取一个适当的正整数，其他条件不变，改求的值。

    查看答案和解析>>


    同步练习册答案