练习册

  • 练习册
  • 试题
    [例1]光滑曲面与竖直平面的交线是抛物线.如图所示.抛物的方程是y=x2.下半部处在一个水平方向的匀强磁场中.磁场的上边界是y=a的直线.一个小金属环从抛物线上y=b处以速度v沿抛物线下滑.假设抛物线足够长.金属环沿抛物线下滑后产生的焦 耳热总量是 ( ) [解析]小金属环进入或离开磁场时.磁通量会发生变化.并产生感应电流.当小金属环全部进入磁场后.不产生感应电流.由能量定恒可得产生的焦耳热等干减少的机械能即 [例2]如图所示.固定在水平绝缘平面上足够长的金属导轨不计电阻.但表面粗糙.导轨左端连接一个电阻R.质量为m的金属棒放在导轨上.并与导轨垂直.整个装置放在匀强磁场中.磁场方向与导轨平面垂直.用水平恒力F把ab棒从静止起向右拉动的过程中①恒力F做的功等于电路产生的电能,②恒力F和摩擦力的合力做的功等于电路中产生的电能,③克服安培力做的功等于电路中产生的电能,④恒力F和摩擦力的合力做的功等于电路中产生的电能和棒获得的动能之和以上结论正确的有 ( ) A．①② B.②③ C．③④ D．②④ [解析]在此运动过程中做功的力是拉力.摩擦力和安培力.三力做功之和为棒ab动能增加量.其中安培力做功将机械能转化为电能.故选项C是正确． [例3]图中a1blcldl和 a2b2c2d2为在同一竖直面内的金属导轨.处在磁感应强度为B的匀强磁场中.磁场方向垂直导轨所在的平面向里.导轨的a1b1段与 a2b2段是竖直的.距离为ll,cldl段与c2d2段也是竖直的.距离为l2. xly1与x2y2为两根用不可伸长的绝缘轻线相连的金属细杆.质量分别为ml和m2.它们都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R.F为作用于金属杆x1yl上的竖直向上的恒力.已知两杆运动到图示位置时.已匀速向上运动.求此时作用于两杆的重力的功率的大小和回路电阻上的热功率. [解析]设杆向上运动的速度为v.因杆的运动.两杆与导轨构成的回路的面积减少.从而磁通量也减少.由法拉第电磁感应定律.回路中的感应电动势的大小ε=B(l2-l1)v①.回路中的电流I=ε/R ②.电流沿顺时针方向.两金属杆都要受到安培力作用.作用于杆x1yl的安培力为f1=Bl1I.③.方向向上.作用于杆x2y2的安培力f2=Bl2I④.方向向下.当杆作匀速运动时.根据牛顿第二定律有F- 本题考查法拉第电磁感应定律.欧姆定律.牛顿运动定律.焦耳定律等规律的综合应用能力． [例4]如下图.在水平面上有两条平行导电导轨MN.PQ.导轨间距离为l.匀强磁场垂直于导轨所在的平面向里.磁感应强度的大小为B.两根金属杆1.2摆在导轨上.与导轨垂直.它们的质量和电阻分别为ml.m2和R1.R2.两杆与导轨接触良好.与导轨间的动摩擦因数为μ.已知:杆1被外力拖动.以恒定的速度v0沿导轨运动,达到稳定状态时.杆2也以恒定速度沿导轨运动.导轨的电阻可忽略.求此时杆2克服摩擦力做功的功率. [解析] 解法一:设杆2的运动速度为v.由于两杆运动时.两杆和导轨构成的回路的磁通量发生变化.产生感应电动势ε=Bl(v0-v) ①.感应电流I=ε/(R1+R2)②.杆2运动受到的安培力等于摩擦力BIl=μm2g ③.导体杆2克服摩擦力做功的功率P=μm2gv ④.解得P=μm2g[v0-μm2g (R1+R2)/B2l2⑤ 解法二:以F表示拖动杆1的外力.表示回路的电流.达到稳定时.对杆1有F-μm1g-BIl①.对杆2有BIl-μm2g=0.②.外力的功率PF=Fv0③.以P表示杆2克服摩 本题主要考查考生应用电磁感应定律.欧姆定律和牛顿运动定律解决力电综合问题的能力． 巩固练习1.如图所示.匀强磁场和竖直导轨所在面垂直.金属棒ab可在导轨上无摩擦滑动.在金属棒.导轨和电阻组成的闭合回路中.除电阻R外.其余电阻均不计.在ab下滑过程中: [ ] A.由于ab下落时只有重力做功.所以机械能守恒． B.ab达到稳定速度前.其减少的重力势能全部转化为电阻R的内能． C.ab达到稳定速度后.其减少的重力势能全部转化为电阻R的内能． D.ab达到稳定速度后.安培力不再对ab做功． 【查看更多】

     

    题目列表(包括答案和解析)

    光滑曲面与竖直平面的交线是抛物线，如图所示，抛物线的方程是y=x2，下半部处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中的虚线所示）．一个小金属块从抛物线上y=b（b＞a）外以速度v沿抛物线下滑．假设抛物线足够长，金属块沿抛物线下滑后产生的焦耳热总量是（　　）

    查看答案和解析>>

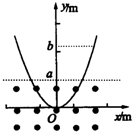    精英家教网光滑曲面与竖直平面的交线是抛物线，抛物线的方程是y=x2，如图所示．下半部处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中的虚线所示）．一个小金属块从抛物线上y=b（b＞a）处从静止开始沿抛物线下滑．假设抛物线足够长，金属块沿抛物线下滑后产生的焦耳热总量是（　　）
    A、mgb
    B、mga
    C、mg（b-a）
    D、mg（b-a）+
    1
    2
    mv2

    查看答案和解析>>

    光滑曲面与竖直平面的交线是抛物线，如图1-3-10所示，抛物线的方程y=kx2，其下半部分处在一水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中的虚线），一个小金属块从抛物线y=b（b＞a）处以速度v沿抛物线下滑，假如抛物线足够长，则金属块在曲面上滑动的过程中产生的焦耳热的总量是(    )

    图1-3-10

    A.mgb                                    B.

    C.mg（b-a）                          D.mg（b-a）+

    查看答案和解析>>

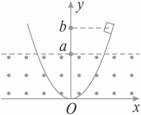
    光滑曲面与竖直平面的交线是抛物线，如图1-3-14所示，抛物线的方程y=kx2，其下半部分处在一水平方向的匀强磁场中，磁场的上边界是y=a的直线(图中的虚线)，一个小金属块从抛物线y=b(b＞a)处以速度v沿抛物线下滑，假如抛物线足够长，则金属块在曲面上滑动的过程中产生的焦耳热的总量是…(    )

    图1-3-14

    A.mgb                          B.mv2

    C.mg(b-a)                    D.mg(b-a)+ mv2

    查看答案和解析>>

    光滑曲面与竖直平面的交线是抛物线，如图2-7所示，抛物线的方程是y=x2，下半部处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中的虚线所示）.一个小金属块从抛物线上y=b（b＞a）处以初速度v沿抛物线下滑.假设抛物线足够长，金属块沿抛物线下滑后产生的焦耳热总量是（　　）

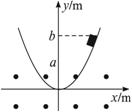
    图2-7

    A.mgb　　B.mv2/2       C.mg（b－a）　　D.mg（b－a）+mv2/2

    查看答案和解析>>


    同步练习册答案