
题目列表(包括答案和解析)
| A.x=1,y=1 | B.x=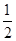 ,y=- ,y=-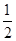 |
C.x=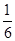 ,y=- ,y=-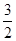 | D.x=-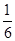 ,y= ,y=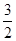 |
[2014·宁化模拟]若向量a=(2x,1,3),b=(1,-2y,9),且a∥b,则( )
| A.x=1,y=1 | B.x=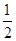 ,y=- ,y=-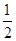 |
C.x= ,y=- ,y=-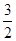 | D.x=- ,y= ,y=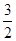 |
| x2 |
| 16 |
| y2 |
| 9 |
| 3 |
| 5 |
给出下列三个命题:①若直线l过抛物线y=2x2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为2;②双曲线C:![]() -
-![]() =-1的离心率为
=-1的离心率为![]() ;③若⊙C1:x2+y2+2x=0,⊙C2:x2+y2+2y-1=0,则这两圆恰有2条公切线.④若直线l1:a2x-y+6=0与直线l2:4x-(a-3)y+9=0互相垂直,则a=-1.
;③若⊙C1:x2+y2+2x=0,⊙C2:x2+y2+2y-1=0,则这两圆恰有2条公切线.④若直线l1:a2x-y+6=0与直线l2:4x-(a-3)y+9=0互相垂直,则a=-1.
其中正确命题的序号是________.(把你认为正确命题的序号都填上)
给出下列三个命题:
①若直线l过抛物线y=2x2的焦点,且与这条抛物线交于A,B两点,则|AB|的最小值为2;
②双曲线C:![]() -
-![]() =-1的离心率为
=-1的离心率为![]() ;
;
③若⊙C1:x2+y2+2x=0,⊙C2:x2+y2+2y-1=0,则这两圆恰有2条公切线.
④若直线l1:a2x-y+6=0与直线l2:4x-(a-3)y+9=0互相垂直,则a=-1.
其中正确命题的序号是________.(把你认为正确命题的序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com