
题目列表(包括答案和解析)
(本小题满分12分)
某客运公司争取到一个相距100海里的甲、乙两地的客运航线权。已知轮船的平均载客人数为200人,轮船每小时使用的燃料费和轮船航行速度的平方成正比,轮船的最大速度为20海里/小时,当船速为10海里/小时,它的燃料费用是每小时60元,其余费用(不论速度如何)总计是每小时150元,假定轮船从甲地到乙地匀速航行。
(I)求轮船每小时的燃料费W与速度v的关系式;
(II)若公司打算从每位乘客身上获得利润10元,那么该公司设计的船票价格最低可以是多少?(精确到1元,参考数据:![]() )
)
(本小题满分12分)
有编号为![]() ,
,![]() ,…
,…![]() 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:

其中直径在区间[1.48,1.52]内的零件为一等品。
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(Ⅱ)从一等品零件中,随机抽取2个.
(ⅰ)用零件的编号列出所有可能的抽取结果;
(ⅱ)求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(本小题满分12分)
有编号为![]() ,
,![]() ,…
,…![]() 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:

其中直径在区间[1.48,1.52]内的零件为一等品。
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(Ⅱ)从一等品零件中,随机抽取2个.
(ⅰ)用零件的编号列出所有可能的抽取结果;
(ⅱ)求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(本小题满分12分)
下表是A市住宅楼房屋销售价格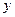 和房屋面积
和房屋面积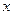 的有关数据:
的有关数据: 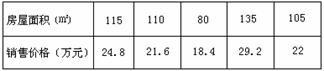
(I)画出数据对应的散点图;
(II)设线性回归方程为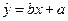 ,已计算得
,已计算得 ,
,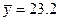 ,计算
,计算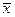 及
及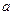 ;
;
(III)据(II)的结果,估计面积为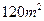 的房屋销售价格.
的房屋销售价格.
(本小题满分12分)
随机抽取某中学甲乙两个班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图(中间的数字表示身高的百位、十位,旁边的数字分别表示身高的个位数)如图所示。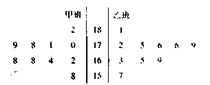
(I)根据茎叶图判断哪个班的平均身高较高;
(II)计算甲班的样本方差;
(III)现从乙班这10名同学中随机抽取两名身高不低于175cm的同学,求身高为176cm的同学被抽中的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com