
题目列表(包括答案和解析)
如果有穷数列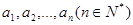 满足条件:
满足条件: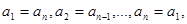
即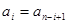 ,
,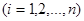 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列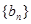 是项数不超过
是项数不超过 的“对称数列”,并使得
的“对称数列”,并使得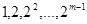 依次为该数列中连续的前
依次为该数列中连续的前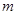 项,则数列
项,则数列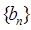 的前2009项和
的前2009项和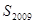 所有可能的取值的序号为
( )
所有可能的取值的序号为
( )
①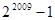 ②
②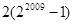 ③
③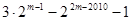 ④
④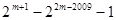
A.①②③ B. ②③④ C.①②④ D. ①③④
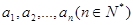 满足条件:
满足条件: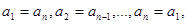
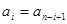 ,
,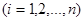 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列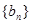 是项数不超过
是项数不超过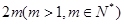 的“对称数列”,并使得
的“对称数列”,并使得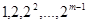 依次为该数列中连续的前
依次为该数列中连续的前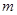 项,则数列
项,则数列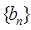 的前2009项和
的前2009项和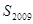 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )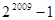 ②
②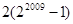 ③
③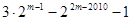 ④
④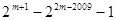
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
如果有穷数列![]() 满足条件:
满足条件:![]() 即
即![]() ,
,![]() 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列![]() 是项数不超过
是项数不超过![]() 的“对称数列”,并使得
的“对称数列”,并使得![]() 依次为该数列中连续的前
依次为该数列中连续的前![]() 项,则数列
项,则数列![]() 的前2009项和
的前2009项和![]() 所有可能的取值的序号为( )
所有可能的取值的序号为( )
①![]() ②
②![]() ③
③![]() ④
④![]()
A.①②③ B. ②③④ C.①②④ D. ①③④
如果有穷数列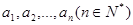 满足条件:
满足条件: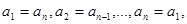
即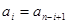 ,
,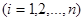 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列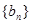 是项数不超过
是项数不超过 的“对称数列”,并使得
的“对称数列”,并使得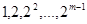 依次为该数列中连续的前
依次为该数列中连续的前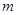 项,则数列
项,则数列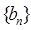 的前2009项和
的前2009项和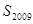 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )
① ②
② ③
③ ④
④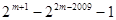
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
如果有穷数列a1,a2,…an(a∈N*)满足条件: ,我们称
,我们称
其为“对称数列”,例如:数列1,2,3,3,2,1和数列1,2,3,4,3,2,1都为“对称数列”。已知数列{bn}是项数不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,……,2m-1依次为该数列中连续的前m项,则数列的前2009项和S2009所有可能的取值的序号为 。
① 22009—1 ②2·(22009—1) ③3×2m-1—22m-2010—1 ④2m+1—22m-2009—1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com