
题目列表(包括答案和解析)
(本小题满分12分)已知函数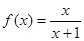 .
.
(Ⅰ)求函数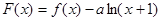 的单调递增区间;
的单调递增区间;
(Ⅱ)数列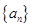 满足:
满足: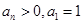 ,且
,且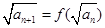 ,记数列
,记数列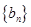 的前n项和为
的前n项和为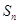 ,
,
且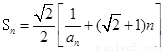 .
.
(ⅰ)求数列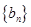 的通项公式;并判断
的通项公式;并判断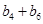 是否仍为数列
是否仍为数列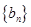 中的项?若是,请证明;否则,说明理由.
中的项?若是,请证明;否则,说明理由.
(ⅱ)设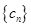 为首项是
为首项是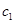 ,公差
,公差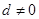 的等差数列,求证:“数列
的等差数列,求证:“数列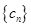 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列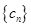 中的项”的充要条件是“存在整数
中的项”的充要条件是“存在整数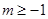 ,使
,使 ”
”
(本小题满分12分)某省份今年是新课标高考的第一年,某校为了充分了解新课标高考,数学备课组从过去2年的新课标各地模拟卷中挑选出50份试卷进行研究,各地挑选的试卷数如下表所示:
|
地区 |
地区A |
地区B |
地区C |
地区D |
|
试卷数 |
20 |
15 |
5 |
10 |
(1)从这50份试卷中随机选出2份,求2份试卷选自同一地区的概率;
(2)若从C、D两地区挑选出2份试卷进行研究,设挑选出地区C的试卷数为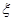 ,求随机变量
,求随机变量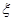 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
设p:实数x满足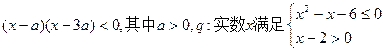
(1)若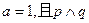 为真,求实数x的取值范围;
为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
(本小题满分12分)
设p:实数x满足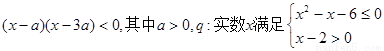
(1)若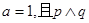 为真,求实数x的取值范围;
为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
(本小题满分12分)
设p:实数x满足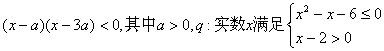
(1)若![]() 为真,求实数x的取值范围;
为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com