（本小题满分12分）

某柑桔基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施；若实施方案一，预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二，预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5； 第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案，第二年与第一年相互独立。令表示方案实施两年后柑桔产量达到灾前产量的倍数。

（1）写出的分布列；

（2）实施哪种方案，两年后柑桔产量超过灾前产量的概率更大？

（3）不管哪种方案，如果实施两年后柑桔产量达不到灾前产量，预计可带来效益10万元；两年后柑桔产量恰好达到灾前产量，预计可带来效益15万元；柑桔产量超过灾前产量，预计可带来效益20万元；问实施哪种方案所带来的平均效益更大？

（本小题满分12分）

全球金融危机，波及中国股市，甲、乙、丙、丁四人打算趁目前股市低迷之际“抄底”，若四人商定在圈定的6只股票中各自随机购买一只（假定购买时每支股票的基本情况完全相同）.

   （1）求甲、乙、丙、丁四人恰好买到同一只股票的概率；

   （2）求甲、乙、丙、丁四人中至多有两人买到同一只股票的概率；

   （3）由于中国政府采取了积极的应对措施，股市渐趋“回暖”.若某人今天按上一交易日的收盘价20元/股，买入某只股票1000股，且预计今天收盘时，该只股票比上一交易日的收盘价上涨10%（涨停）的概率为0.6.持平的概率为0.2，否则将下跌10%（跌停）,求此人今天获利的数学期望（不考虑佣金、印花税等交易费用）.

（本小题满分12分）
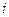某柑桔基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施；若实施方案一，预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二，预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案，第二年与第一年相互独立。令表示方案实施两年后柑桔产量达到灾前产量的倍数。
（1）写出的分布列；
（2）实施哪种方案，两年后柑桔产量超过灾前产量的概率更大？
（3）不管哪种方案，如果实施两年后柑桔产量达不到灾前产量，预计可带来效益10万元；两年后柑桔产量恰好达到灾前产量，预计可带来效益15万元；柑桔产量超过灾前产量，预计可带来效益20万元；问实施哪种方案所带来的平均效益更大？

（本小题满分12分）

国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：

（Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少?

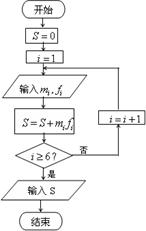
（Ⅱ）该网站利用右边的算法流程图，对样本数据作进一步统计分析，求输出的S的值，并说明S的统计意义。

（本小题满分12分）甲、乙、丙三台机床各自独立地加工同一种零件，已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为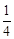，乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为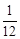，甲、丙两台机床加工的零件都是一等品的概率为.

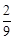（Ⅰ）分别求甲、乙、丙三台机床各自加工的零件是一等品的概率；

（Ⅱ）若让每台机床各自加工2个零件（共计6个零件），求恰好有3个零件是一等品的概率.