（(本题15分)

在平面直角坐标系xOy中，已知点A(0,0)，B(-2,0)，C(-2,1)。设k为非零实数，矩阵M=,N=，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B1C1的面积是△ABC面积的2倍，

（1）求k的值。

（2）判断变换MN是否可逆，如果可逆，求矩阵MN的逆矩阵；如不可逆，说明理由．

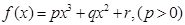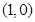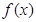(本题15分)已知函数图象的对称中心为，且的极小值为.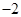

（1）求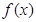的解析式；

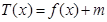（2）设，若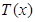有三个零点，求实数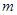的取值范围；

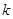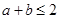（3）是否存在实数，当时，使函数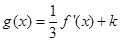

在定义域[a,b] 上的值域恰为[a,b]，若存在，求出k的范围；若不存在，说明理由.

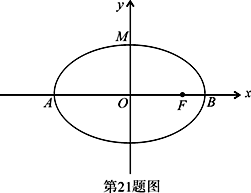
（本题15分）如图，椭圆长轴端点为，为椭圆中心，为椭圆的右焦点,且，．（1）求椭圆的标准方程；（2）记椭圆的上顶点为，直线交椭圆于两点，问：是否存在直线，使点恰为的垂心？若存在，求出直线的方程;若不存在，请说明理由.

（本题15分）某租赁公司拥有汽车100辆．当每辆车的月租金为3000元时，可全部租出．若每辆车的月租金每增加50元，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．

（１）当每辆车的月租金定为3600元时,能租出多少辆车?（２）当每辆车的月租金定为多少元时, 租赁公司的月收益最大，最大月收益是多少?

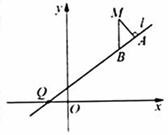
（08年浙江卷）（本题15分）已知曲线是到点和到直线距离相等的点的轨迹．是过点的直线，是上（不在上）的动点；在上，，轴（如图）．

（Ⅰ）求曲线的方程；

（Ⅱ）求出直线的方程，使得为常数．