如图所示，水平光滑地面上停放着一辆质量为M的小车，小车左端靠在竖直墙壁上，其左侧半径为R的四分之一圆弧轨道AB是光滑的，轨道最低点B与水平轨道BC相切，整个轨道处于同一竖直平面内．将质量为m的物块（可视为质点）从A点无初速度释放，物块沿轨道滑行至轨道末端C处恰好没有滑出．重力加速度为g，空气阻力可忽略不计．关于物块从A位置运动至C位置的过程，下列说法中正确的是（　　）

A．在这个过程中，小车和物块构成的系统水平方向动量守恒

B．在这个过程中，物块克服摩擦力所做的功为mgR

C．在这个过程中，摩擦力对小车所做的功为mgR

D．在这个过程中，由于摩擦生成的热量为 mMgR M+m

查看答案和解析>>

如图所示，水平光滑地面上停放着一辆小车，左侧靠在竖直墙壁上，光滑圆弧轨道AB的最低点B与足够长的水平轨道相切，整个轨道处于同一竖直平面内．可视为质点的物块从A点正上方H处无初速度下落，恰好落入小车圆弧轨道，并沿半径为R的四分之一圆弧轨道滑下，最终小车与物块一起运动．已知小车的质量为M，物块的质量为m，不考虑空气阻力和物块落入圆弧轨道时的能量损失，（重力加速度用g表示）．求：
（1）物块到达B点时的速度大小？
（2）物块到达圆弧轨道最低点B时，轨道对它的支持力的大小？
（3）物块和小车的最终速度大小？

查看答案和解析>>

如图所示，水平光滑地面上停放着一辆小车，左侧靠在竖直墙壁上，小车的四分之一圆弧轨道AB是光滑的，在最低点B与水平轨道BC相切，BC的长度是圆弧半径R的10倍，整个轨道处于同一竖直平面内．可视为质点的物块在上方某处无初速下落，恰好落入小车圆弧轨道，然后沿水平轨道滑行至轨道末端C处恰好没有滑出．已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍，小车的质量是物块的3倍，不考虑空气阻力和物块落入圆弧轨道时的能量损失．求：
（1）物块开始下落的位置距水平轨道BC的竖直高度？
（2）物块与水平轨道BC间的动摩擦因数μ．

查看答案和解析>>

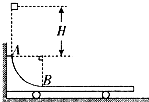如图所示，水平光滑地面上停放着一辆小车，左侧靠在竖直墙壁上，光滑四分之一圆弧轨道AB的最低点B与足够长的水平粗糙轨道相切，整个轨道处于同一竖直平面内．可视为质点的物块从A点正上方H处无初速度下落，恰好落入小车圆弧轨道，并沿半径为R的四分之一圆弧轨道滑下，最终小车与物块一起运动．已知小车的质量为M，物块的质量为m，不考虑空气阻力和物块落入圆弧轨道时的能量损失（重力加速度用g表示）．求：
（1）物块到达圆弧轨道最低点B时，轨道对它的支持力的大小；
（2）小车的最终速度为多大？
（3）全过程墙壁对小车的冲量为多大：

查看答案和解析>>

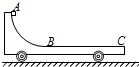如图所示，水平光滑地面上停放着一辆质量为M的小车，其左侧半径为R的四分之一圆弧轨道AB是光滑的，轨道最低点B与水平轨道BC相切，整个轨道处于同一竖直平面内．将质量为m的物块（可视为质点）从A点无初速释放，物块沿轨道滑行至轨道末端C处恰好没有滑出．重力加速度为g，空气阻力可忽略不计．关于物块从A位置运动至C位置的过程，下列说法中正确的是（　　）

A、小车和物块构成的系统动量守恒

B、摩擦力对物块和轨道BC所做功的代数和为零

C、物块的最大速度为 2gR

D、小车的最大速度为 2m2gR M2+Mm

查看答案和解析>>

一．选择题：

1.CD

2.A

3.C

4.CD

5.ABC

6.BD 

7.B

8.AD 

9.D

10.B 

11.A 

12.D

13.C

二．实验题

14．  C  F     A D   

15. 375       I       R₀ 

16．B    D   ，电路图为变阻器分压，电流表外接，连线略

17．若横轴为R（电路为电压表和电阻箱串联，接上电源开关），则    若横轴为（电路为电压表和电阻箱并联，接上电源开关），则，

三计算题

18．解：（1）当B最小时，安培力最小沿斜面向上，由左手定则可知，B的方向垂直斜面向上，由平衡条件可得F_安=mgsinα, F_安=BIL。所以

（2）无压力时，F_安=mg，，由左手定则可知，B的方向水平向左。

19．解：由图得：a＝＝0.5m/s²，

前2s有：F₂－mg sina＝ma，2s后有：F₂＝mg sina，代入数据可解得：m＝1kg，a＝30°。

20．解：（1）设物块的质量为m，其开始下落处的位置距BC的竖直高度为h，到达B点时的速度为v，小车圆弧轨道半径为R。由机械能守恒定律，有：mgh=mv²

根据牛顿第二定律，有：9mg－mg=m解得h=4R

则物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍。

（2）设物块与BC间的滑动摩擦力的大小为F，物块滑到C点时与小车的共同速度为v'，物块在小车上由B运动到C的过程中小车对地面的位移大小为s。依题意，小车的质量为3m，BC长度为10R。由滑动摩擦力有：  F=μmg

由动量守恒定律，有mv=(m+3m)v^/  对物块、小车分别应用动能定理，有

－F(10R+s)=mv^/2 －mv²    Fs=(3m)v^/2－0   μ＝0.3

21.解：粒子在电场中做类平抛运动，竖直速度V_y=at，加速度

水平位移L=V₀t，由以上各式得进入电场时的合速度为，方向与y轴成45⁰，

（2）带电粒子在磁场中做匀速圆周运动  ，与右边界相切时，由几何关系得Rsin45⁰+R=d,解得，故磁场的宽度最大为