练习册

  • 练习册
  • 试题
    ＜＜2.∴1＜＜.同理可得.1＜＜.猜想1＜＜().--------下面用数学归纳法证明:(1)当n=2时.前面已证: 【查看更多】

     

    题目列表(包括答案和解析)

    设集合M是满足下列条件的函数f（x）的集合：①f（x）的定义域为R；②存在a＜b，使f（x）在（-∞，a），（b，+∞）上分别单调递增，在（a，b）上单调递减．
    （I）设f1（x）=x•|x-2|，f2（x）=x3-3x2+3x，判断f1（x），f2（x）是否在集合M中，并说明理由；
    （II）求证：对任意的实数t，f（x）=
    -x+tx2+1
    都在集合M中；
    （Ⅲ）是否存在可导函数f（x），使得f（x）与g（x）=f'（x）-x都在集合M中，并且有相同的单调区间？请说明理由．

    查看答案和解析>>

    定理：已知O，A，B三点不共线，若点P在直线AB上，且
    OP
    =λ
    OA
    λ2
    OB
    则λ1+λ2=1，类比该定理进行研究，可以得出：已知O、A、B三点不共线，若点P、O在直线AB同侧（点P不在直线AB上），且
    OP
    =λ1
    OA
    λ2
    OB
    ，则
    λ1+λ2＜1
    λ1+λ2＜1
    ．

    查看答案和解析>>

    给出下列四个结论：

    ①合情推理是由特殊到一般的推理，得到的结论不一定正确，演绎推理是由一般到特殊的推理，得到的结论一定正确．

    ②甲、乙两同学各自独立地考察两个变量X、Y的线性相关关系时，发现两人对X的观察数据的平均值相等，都是s，对Y的观察数据的平均值也相等，都是t，各自求出的回归直线分别是l1、l2，则直线l1与l2必定相交于点(s，t)．

    ③用独立性检验(2×2列联表法)来考察两个分类变量是否有关系时，算出的随机变量K2的值越大，说明“X与Y有关系”成立的可能性越大．

    ④命题P：x∈R，使得x2＋x＋1＜0，则P：x∈R均有x2＋x＋1≥0．

    其中结论正确的序号为________．(请写出你认为正确的所有结论的序号)

    查看答案和解析>>

    (理)如图a所示，某地为了开发旅游资源，欲修建一条连接风景点P和居民区O的公路，点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°＜θ＜90°)，且sinθ=，点P到平面α的距离PH=0．4(km)．沿山脚原有一段笔直的公路AB可供利用．从点O到山脚修路的造价为a万元／km，原有公路改建费用为万元／km．当山坡上公路长度为l km(1≤l≤2)时，其造价为(l2+1)a万元已知OA⊥AB，PB⊥AB，AB=1．5(km)，OA=(km)．

    (1)在AB上求一点D，使沿折线PDAO修建公路的总造价最小；

    (2)对于(1)中得到的点D，在DA上求一点E，使沿折线PDEO修建公路的总造价最小；

    (3)在AB上是否存在两个不同的点D′，E′，使沿折线．PD′E′O修建公路的总造价小于(2)中得到的最小总造价?证明你的结论．

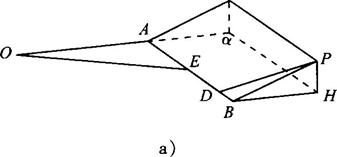
    a)

    第19题图

    (文)如图b所示，直四棱柱ABCD-A1B1C1D1中，∠ADC=90°，△ABC为等边三角形，且AA1=AD=DC=2．

    (1)求AC1与BC所成角的余弦值；

    (2)求二面角C1-BD-C的大小；

    (3)设M是BD上的点，当DM为何值时，D1M⊥平面A1C1D?并证明你的结论．

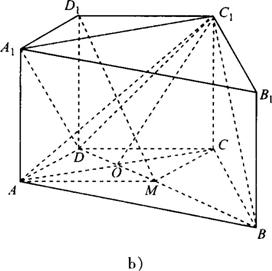
    第19题图

    查看答案和解析>>

    对于数列{xn}，从中选取若干项，不改变它们在原来数列中的先后次序，得到的数列称为是原来数列的一个子数列．某同学在学习了这一个概念之后，打算研究首项为a1，公差为d的无穷等差数列{an}的子数列问题，为此，他取了其中第一项a1，第三项a3和第五项a5．
    （1）若a1，a3，a5成等比数列，求d的值；
    （2）在a1=1，d=3 的无穷等差数列{an}中，是否存在无穷子数列{bn}，使得数列（bn）为等比数列？若存在，请给出数列{bn}的通项公式并证明；若不存在，说明理由；
    （3）他在研究过程中猜想了一个命题：“对于首项为正整数a，公比为正整数q（q＞1）的无穷等比数列{cn}，总可以找到一个子数列{bn}，使得{dn}构成等差数列”．于是，他在数列{cn}中任取三项ck，cm，cn（k＜m＜n），由ck+cn与2cm的大小关系去判断该命题是否正确．他将得到什么结论？

    查看答案和解析>>


    同步练习册答案