
题目列表(包括答案和解析)
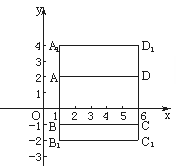
 各点的坐标分别为A(1,2),B(1,-1),C(6,-1),D(6,2),则AB= ,BC= ,S
各点的坐标分别为A(1,2),B(1,-1),C(6,-1),D(6,2),则AB= ,BC= ,S =_____.
=_____.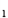 B
B C
C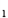 D
D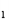 ,A
,A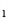 (1,4), B
(1,4), B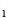 (1,-2), C
(1,-2), C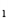 (6,-2),
(6,-2), D
D (6,4),则A
(6,4),则A B
B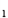 =_____B
=_____B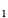 C
C = ,S
= ,S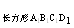 =_____.显然S
=_____.显然S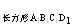 =2 S
=2 S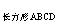 ,
, 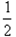 ,面积也就会变为原来的
,面积也就会变为原来的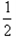 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com