
题目列表(包括答案和解析)
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产。已知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目 类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 20 |
| 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关,![]() 为常数,且
为常数,且![]() 。另外,年销售
。另外,年销售![]() 件B产品时需上交
件B产品时需上交![]() 万美元的特别关税。
万美元的特别关税。
(1)写出该厂分别投资生产A、B两种产品的年利润![]() ,
,![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系并指明其定义域;
之间的函数关系并指明其定义域;
(2)如何投资才可获得最大年利润。
| 项目 类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 20 |  | 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
 为常数,且
为常数,且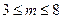 。另外,年销售
。另外,年销售 件B产品时需上交
件B产品时需上交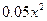 万美元的特别关税。
万美元的特别关税。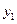 ,
,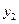 与生产相应产品的件数
与生产相应产品的件数 之间的函数关系并指明其定义域;
之间的函数关系并指明其定义域;| 产品数量x(百件) | 6 | 10 | 20 |
| 成本合计y(千元) | 104 | 160 | 370 |
商场销售某种商品的经验表明,该商品每日的销售量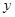 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式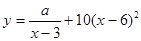 ,其中
,其中 ,
, 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求 的值;
的值;
(2) 若商品的成品为3元/千克, 试确定销售价格 的值,使商场每日销售该商品所获得的利润最大
的值,使商场每日销售该商品所获得的利润最大
【解析】(1)利用销售价格为5元/千克时,每日可售出该商品11千克.把x=5,y=11代入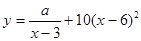 ,解关于a的方程即可求a..
,解关于a的方程即可求a..
(2)在(1)的基础上,列出利润关于x的函数关系式,
利润=销售量 (销售单价-成品单价),然后利用导数求其最值即可.
(销售单价-成品单价),然后利用导数求其最值即可.
某工厂统计资料显示,一年中总产品次品率P与日产量![]() 件之间的关系如下表所示:
件之间的关系如下表所示:
| 日产量 | 80 | 81 | 82 | … |
| … | 98 | 99 | 100 |
| 次品率 |
|
|
| … |
| … |
|
|
|
其中![]() (a为常数),已知生产一件正品赢利k元,生产一件次品损失
(a为常数),已知生产一件正品赢利k元,生产一件次品损失![]() 元
元
(![]() 为给定常数).
为给定常数).
(Ⅰ)求出a,并将该厂的日盈利额y(元)表示为日生产量x(件)的函数;
(Ⅱ)为获取最大盈利,该厂的日生产量应定为多少件?
一、选择题
1―8 DAACA CBD
二、填空题
9. 10.
10. 11.
11. 12.
12. 13.50 14.5
13.50 14.5
三、解答题
15.(本小题满分13分)
解:(1)由 ………………2分
………………2分
整理得
即 ……………………3分
……………………3分
又 ……………………5分
……………………5分
又因为 ,
,
所以 …………………………6分
…………………………6分
(2)因为 ,所以
,所以
故 …………………………7分
…………………………7分
由
即 ,
,
所以 .
.
即 .……………………11分
.……………………11分
因为 ……………………12分
……………………12分
故
所以 ……………………13分
……………………13分
16.(本小题满分13分)
解:(1)取AC的中点O,连结OS,OB。
∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥OB。又平面SAC⊥平面ABC,且平面SAC∩平面ABC=BC,
∴SO⊥平面ABC。
故SB在平面ABC内的射影为OB。
∴AC⊥SB.……………………6分
(2)取OB的中点D,作NE⊥CM交GM于E,连结DE,ND。
在△SOB中,N、D分别为SB,OB的中点,
∴DN//SO,又SO⊥平面ABC,
∴DN⊥平面ABC,由NE⊥CM得DE⊥CM。
故∠NED为二面角N―CM―B的平面角,………………9分
设OB与CM交于G,则G为△ABC的中心
∴ DE⊥CM,BM⊥CM,
DE⊥CM,BM⊥CM,
|